题目内容
我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”,己知 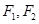 是一对相关曲线的焦点,P是它们在第一象限的交点,当
是一对相关曲线的焦点,P是它们在第一象限的交点,当 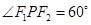 ,则这 一对相关曲线中椭圆的离心率是________.
,则这 一对相关曲线中椭圆的离心率是________.

解析试题分析:设F1P=m,F2P=n,F1F2=2c,由余弦定理得(2c)2=m2+n2-2mncos60°,即4c2=m2+n2-mn,①
设a1是椭圆的实半轴,a2是双曲线的实半轴,由椭圆及双曲线定义,得m+n=2a1,m-n=2a2,
∴m=a1+a2,n=a1-a2,代入①得, ,②
,②
由离心率互为倒数知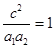 ,所以
,所以 =
= ,代入②式得整理得,
,代入②式得整理得, ,
,
两边同除以 得,
得, ,解得
,解得 =
=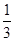 或
或 =1(舍),所以椭圆的离心率为
=1(舍),所以椭圆的离心率为 =
= .
.
考点:椭圆定义与性质,双曲线定义与性质,余弦定理,对新概念的理解和应用,转化与化归思想

练习册系列答案
相关题目
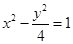 有共同的渐近线,且过点
有共同的渐近线,且过点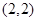 的双曲线方程是________.
的双曲线方程是________.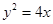 的焦点为顶点,顶点为中心,离心率为2的双曲线方程是 .
的焦点为顶点,顶点为中心,离心率为2的双曲线方程是 .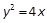 上的一点,F为抛物线的焦点,A在圆C:
上的一点,F为抛物线的焦点,A在圆C: 上,则
上,则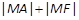 的最小值为__________.
的最小值为__________.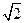
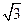
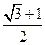
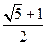
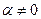 的直线
的直线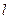 过椭圆
过椭圆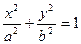
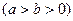 的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则
的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则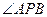 为( )
为( )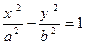 与椭圆
与椭圆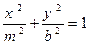 (
(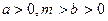 )的离心率之积大于1,则以
)的离心率之积大于1,则以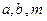 为边长的三角形一定是( )
为边长的三角形一定是( )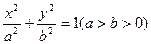 的左右焦点分别为F1、F2,线段F1F2被抛物线
的左右焦点分别为F1、F2,线段F1F2被抛物线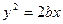 的焦点分成5∶3的两段,则此椭圆的离心率为( )
的焦点分成5∶3的两段,则此椭圆的离心率为( )
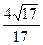
 的右焦点重合,则该抛物线的准线方程为___________.
的右焦点重合,则该抛物线的准线方程为___________.