题目内容
已知命题p:“?x∈[1,2],x2-a≥0”;命题q:“?x∈R,x2+2ax+2-a=0”.若命题“p且q”是真命题,则实数a的取值范围为( )
| A.a≤-2或a=1 |
| B.a≤-2或1≤a≤2 |
| C.a≥1 |
| D.-2≤a≤1 |
A
由已知可知p和q均为真命题.
若x∈[1,2],则x2∈[1,4],
由x2-a≥0
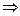 a≤x2∴命题p为真得a≤1,
a≤x2∴命题p为真得a≤1,又命题q为真得,所以△=4a2-4(2-a)≥0,即a≤-2或a≥1,
综合得a≤-2或a=1.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 :方程
:方程 有两个不相等的负实根,命题
有两个不相等的负实根,命题 :
:
 恒成立;若
恒成立;若 的取值范围.
的取值范围.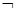 p)∧(
p)∧( ,
, ”的否定是:“不存在
”的否定是:“不存在 ”;
”; 的零点在区间
的零点在区间 内;
内;  的图象的切线的斜率的最大值是
的图象的切线的斜率的最大值是 ;
; 恒过样本中心
恒过样本中心 ,且至少过一个样本点.
,且至少过一个样本点.



 ”的否定是( )
”的否定是( )



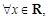
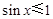 ”的否定是“ ”.
”的否定是“ ”.