题目内容
已知函数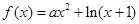 .
.
(1) 当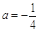 时,求函数
时,求函数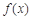 的单调区间;
的单调区间;
(2) 当 时,函数
时,函数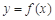 图象上的点都在
图象上的点都在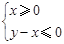 所表示的平面区域内,求实数
所表示的平面区域内,求实数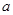 的取值范围.
的取值范围.
【答案】
(1) 函数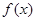 的单调递增区间为
的单调递增区间为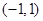 ,单调递减区间为
,单调递减区间为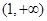 ;(2)
;(2)  .
.
【解析】
试题分析:本小题主要通过函数与导数综合应用问题,具体涉及到用导数来研究函数的单调性等知识内容,考查考生的运算求解能力,推理论证能力,其中重点对导数对函数的描述进行考查,本题是一道难度较高且综合性较强的压轴题,也是一道关于数列拆分问题的典型例题,对今后此类问题的求解有很好的导向作用.(1)代入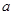 的值,明确函数解析式,并注明函数的定义域,然后利用求导研究函数的单调性;(2)利用构造函数思想,构造
的值,明确函数解析式,并注明函数的定义域,然后利用求导研究函数的单调性;(2)利用构造函数思想,构造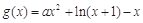 ,然后利用转化思想,将问题转化为只需
,然后利用转化思想,将问题转化为只需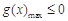 ,下面通过对
,下面通过对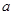 进行分类讨论进行研究函数的单调性,明确最值进而确定
进行分类讨论进行研究函数的单调性,明确最值进而确定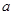 的取值范围.
的取值范围.
试题解析:(1) 当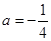 时,
时,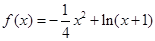
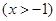 ,
,
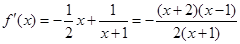
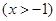 ,
,
由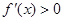 解得
解得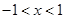 ,由
,由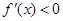 解得
解得 .
.
故函数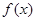 的单调递增区间为
的单调递增区间为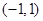 ,单调递减区间为
,单调递减区间为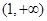 . (6分)
. (6分)
(2) 因函数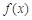 图象上的点都在
图象上的点都在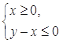 所表示的平面区域内,
所表示的平面区域内,
则当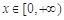 时,不等式
时,不等式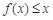 恒成立,即
恒成立,即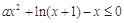 恒成立,、
恒成立,、
设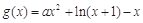 (
(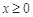 ),只需
),只需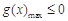 即可.
即可.
由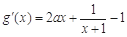
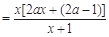 ,
,
(i) 当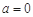 时,
时,
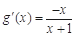 ,
,
当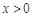 时,
时,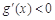 ,函数
,函数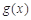 在
在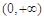 上单调递减,故
上单调递减,故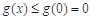 成立.
成立.
(ii) 当 时,由
时,由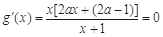 ,因
,因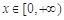 ,所以
,所以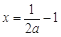 ,
,
① 若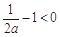 ,即
,即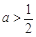 时,在区间
时,在区间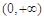 上,
上,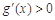 ,
,
则函数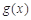 在
在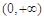 上单调递增,
上单调递增,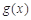 在
在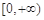 上无最大值,当
上无最大值,当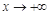 时,
时, 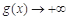 ,此时不满足条件;
,此时不满足条件;
② 若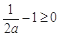 ,即
,即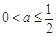 时,函数
时,函数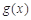 在
在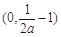 上单调递减,
上单调递减,
在区间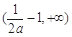 上单调递增,同样
上单调递增,同样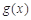 在
在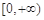 上无最大值,当
上无最大值,当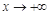 时,
时, 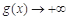 ,不满足条件.
,不满足条件.
(iii) 当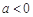 时,由
时,由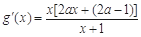 ,∵
,∵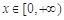 ,∴
,∴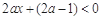 ,
,
∴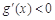 ,故函数
,故函数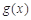 在
在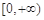 上单调递减,故
上单调递减,故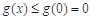 成立.
成立.
综上所述,实数a的取值范围是 .
(12分)
.
(12分)
考点:(1)函数的单调区间;(2)导数的应用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目