题目内容
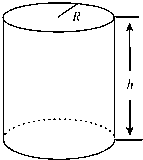 圆柱型金属饮料罐的容积V一定时,它的高h与底面半径R具有怎样的关系时,才能使所用材料最省?
圆柱型金属饮料罐的容积V一定时,它的高h与底面半径R具有怎样的关系时,才能使所用材料最省?
(本小题满分12分)
解:如图,饮料罐的表面积S=2πRh+2πR2.…(2分)
由V=πR2h,得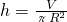 ,则
,则
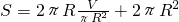 =
=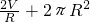 .(R>0)…(4分)
.(R>0)…(4分)
所以S=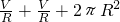
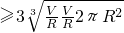 =3
=3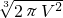 ,
,
当且仅当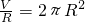 ,即
,即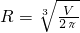 时,S取得最小值.…(10分)
时,S取得最小值.…(10分)
把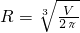 代入
代入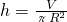 ,得
,得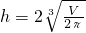 ,即h=2R.…(11分)
,即h=2R.…(11分)
答:当饮料罐的高与底面的直径相等时,所用材料最省. …(12分)
分析:由题意求出饮料罐的表面积,求出体积,推出表面积与圆柱底面半径的关系式,通过不等式求出面积的最小值.
点评:本题是中档题,考查圆柱的表面积与体积的关系,不等式的应用,考查计算能力.
解:如图,饮料罐的表面积S=2πRh+2πR2.…(2分)
由V=πR2h,得
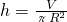 ,则
,则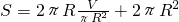 =
=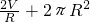 .(R>0)…(4分)
.(R>0)…(4分)所以S=
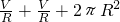
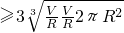 =3
=3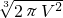 ,
,当且仅当
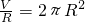 ,即
,即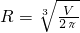 时,S取得最小值.…(10分)
时,S取得最小值.…(10分)把
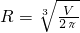 代入
代入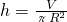 ,得
,得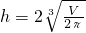 ,即h=2R.…(11分)
,即h=2R.…(11分)答:当饮料罐的高与底面的直径相等时,所用材料最省. …(12分)
分析:由题意求出饮料罐的表面积,求出体积,推出表面积与圆柱底面半径的关系式,通过不等式求出面积的最小值.
点评:本题是中档题,考查圆柱的表面积与体积的关系,不等式的应用,考查计算能力.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
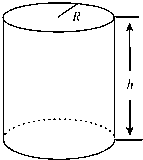 (2011•武昌区模拟)圆柱型金属饮料罐的容积V一定时,它的高h与底面半径R具有怎样的关系时,才能使所用材料最省?
(2011•武昌区模拟)圆柱型金属饮料罐的容积V一定时,它的高h与底面半径R具有怎样的关系时,才能使所用材料最省?