题目内容
请先用文字叙述两个平面平行的性质定理,然后写出已知、求证、画出图象并写出证明过程.
分析:两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.证明此命题可用反证法,由于交线在同一平面内,故只需假设两交线相交,推出矛盾即可
解答:解:两个平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
已知:如图,α∥β,α∩γ=a,β∩γ=b,求证:a∥b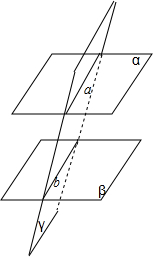
证明:假设直线a与直线b相交,且a∩b=O
∵a?α,O?a,
∴O?α
同理,O?β
即α与β有公共点O,
这与已知α∥β矛盾
假设不成立,直线a与直线b不相交
∵a?γ,b?γ
∴a∥b
已知:如图,α∥β,α∩γ=a,β∩γ=b,求证:a∥b

证明:假设直线a与直线b相交,且a∩b=O
∵a?α,O?a,
∴O?α
同理,O?β
即α与β有公共点O,
这与已知α∥β矛盾
假设不成立,直线a与直线b不相交
∵a?γ,b?γ
∴a∥b
点评:本题考查了面面平行的性质定理的记忆、理解、及证明,证明命题的规范,反证法的运用

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
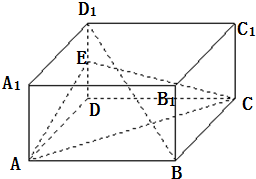 如图,在长方体ABCD-A1B1C1D1中,E是DD1的中点.
如图,在长方体ABCD-A1B1C1D1中,E是DD1的中点.