题目内容
19.已知异面直线a与b所成角为θ,P为空间一点,过点P作直线l使l和a、b所成角相等,此等角记为β,β≥$\frac{θ}{2}$,且β∈(0°,90°],则直线l的条数构成的集合为{1,2,3,4}.分析 可以过P点分别作这两异面直线的平行线a1,b1,根据l在直线a1,b1的夹角的平分线上时,与a1,b1的夹角最小,从而分$β=\frac{θ}{2},\frac{θ}{2}<β<\frac{π-θ}{2},β=\frac{π-θ}{2}$,和$\frac{π-θ}{2}<β<\frac{π}{2}$,以及$β=\frac{π}{2}$五种情况,求出每种情况对应的直线l的条数,从而得出直线l的条数构成的集合.
解答 解:如图,已知异面直线a,b,过点P作a1∥a,b1∥b,则相交直线a1,b1确定一平面α,a1与b1夹角为θ或π-θ;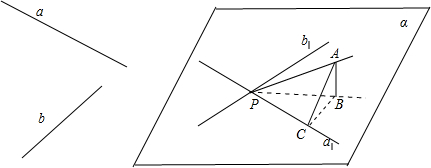
在直线l取点A,过A作AB⊥α,垂足为B,作BC⊥a1,垂足为C;
则$∠BPC=\frac{θ}{2}$,或$\frac{π-θ}{2}$,∠APC=β,设∠APB=θ1,∠BPC=θ2则:cosβ=cosθ1cosθ2;
∵0≤θ1≤$\frac{π}{2}$,∴0≤cosβ≤cosθ2;
当θ2=$\frac{θ}{2}$时,由0≤cosβ≤cos$\frac{θ}{2}$,得$\frac{θ}{2}$≤β≤$\frac{π}{2}$;
当θ2=$\frac{π-θ}{2}$时,由0≤cosβ≤cos$\frac{π-θ}{2}$,得$\frac{π-θ}{2}≤β≤\frac{π}{2}$;
∴$β=\frac{θ}{2}$时,l只有1条,$\frac{θ}{2}<β<\frac{π-θ}{2}$时,l有2条,$β=\frac{π-θ}{2}$时,l有3条,$\frac{π-θ}{2}<β<\frac{π}{2}$时,l有4条,$β=\frac{π}{2}$时,有1条;
∴直线l的条数构成的集合为:{1,2,3,4}.
故答案为:{1,2,3,4}.
点评 考查异面直线所成角的定义,异面直线所成角的范围,知道过一角的顶点并和该角的两边所成角相等的直线在该角所在平面内的射影在该角的角平分线上.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案