题目内容
过点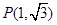 作圆
作圆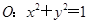 的两条切线,切点分别为
的两条切线,切点分别为 和
和 ,则弦长
,则弦长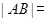 ( )
( )
A.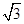 | B. | C. | D.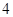 |
A
解析试题分析:如图所示
∵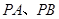 分别为圆
分别为圆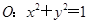 的切线,
的切线,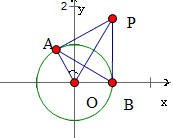
∴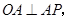
∵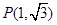 ,
,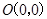 ,∴
,∴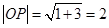 ,
,
又∵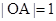 ,在
,在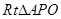 中,
中,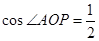 ,
,
∴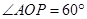 ,∴
,∴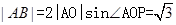 .
.
故选 .
.
考点:直线与圆的位置关系,勾股定理

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线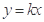 与圆
与圆 的两个交点关于直线
的两个交点关于直线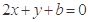 对称,则
对称,则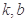 的值分别为( )
的值分别为( )
A.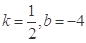 | B.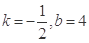 |
C.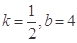 | D.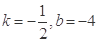 |
已知圆的方程为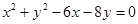 .设该圆过点
.设该圆过点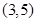 的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A.10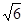 | B.20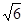 | C.30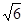 | D.40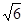 |
圆 关于直线
关于直线 对称的圆的方程为( )
对称的圆的方程为( )
A. | B. |
C. | D. |
直线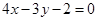 与圆
与圆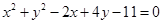 的位置关系是( )
的位置关系是( )
| A.相离 | B.相切 | C.相交过圆心 | D.相交不过圆心 |
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5 -4 -4 | B.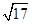 -1 -1 |
C.6-2 | D.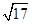 |
过点A(11,2)作圆x2+y2+2x-4y-164=0的弦,其中弦长为整数的共有( )
| A.16条 | B.17条 | C.32条 | D.34条 |
若直线y=kx与圆(x-2)2+y2=1的两个交点关于直线2x+y+b=0对称,则k,b的值分别为( )
A.k=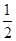 ,b=-4 ,b=-4 | B.k=-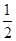 ,b=4 ,b=4 | C.k=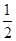 ,b=4 ,b=4 | D.k=-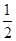 ,b=-4 ,b=-4 |
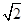 ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).