题目内容
已知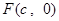 是椭圆
是椭圆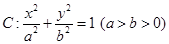 的右焦点,圆
的右焦点,圆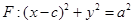 与
与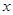 轴交于
轴交于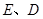 两点,
两点,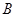 是椭圆
是椭圆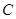 与圆
与圆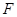 的一个交点,且
的一个交点,且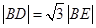
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)过点 与圆
与圆 相切的直线
相切的直线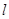 与
与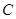 的另一交点为
的另一交点为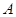 ,且
,且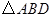 的面积为
的面积为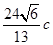 ,求椭圆
,求椭圆 的方程
的方程
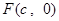 是椭圆
是椭圆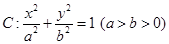 的右焦点,圆
的右焦点,圆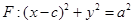 与
与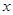 轴交于
轴交于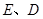 两点,
两点,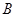 是椭圆
是椭圆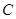 与圆
与圆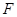 的一个交点,且
的一个交点,且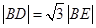
(Ⅰ)求椭圆
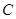 的离心率;
的离心率;(Ⅱ)过点
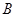 与圆
与圆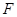 相切的直线
相切的直线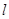 与
与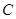 的另一交点为
的另一交点为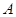 ,且
,且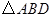 的面积为
的面积为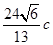 ,求椭圆
,求椭圆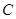 的方程
的方程 (Ⅰ) ;(Ⅱ)
;(Ⅱ)
 ;(Ⅱ)
;(Ⅱ)
试题分析:(Ⅰ)根据椭圆的定义、几何性质可求;(Ⅱ)直线与椭圆相交,联立消元,设点代入化简,利用点到直线的距离来求
试题解析:(Ⅰ)由题意,
 ,
, ,
,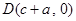 ,
,∵
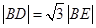 ,
,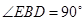 ,得
,得 ,
,由
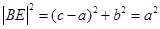 , 得
, 得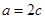 ,
,即椭圆
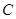 的离心率
的离心率 (4分)
(4分)(Ⅱ)
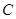 的离心率
的离心率 ,令
,令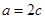 ,
, ,则
,则
直线
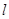
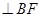 ,设
,设
由
 得
得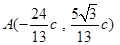 ,
,
又点
 到直线
到直线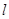 的距离
的距离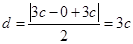 ,
,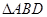 的面积
的面积
 , 解得
, 解得
故椭圆
 (12分)
(12分)
练习册系列答案
相关题目
 :
: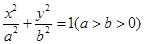 的离心率为
的离心率为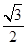 ,以椭圆
,以椭圆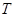 为圆心作圆
为圆心作圆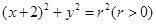 ,设圆
,设圆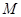 与点
与点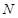 .(12分)
.(12分)
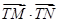 的最小值,并求此时圆
的最小值,并求此时圆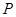 是椭圆
是椭圆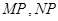 分别与
分别与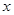 轴交于点
轴交于点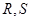 ,
,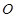 为坐标原点,求证:
为坐标原点,求证: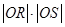 为定值.(5分)
为定值.(5分)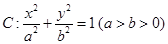 经过点
经过点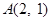 ,离心率为
,离心率为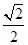 ,过点
,过点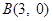 的直线
的直线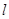 与椭圆
与椭圆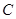 交于不同的两点
交于不同的两点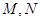 .
.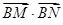 的取值范围.
的取值范围.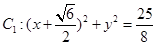 ,圆
,圆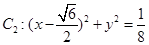 ,动圆
,动圆 与已知两圆都外切.
与已知两圆都外切. 的方程;
的方程;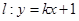 与点
与点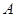 、
、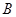 ,
,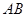 的中垂线与
的中垂线与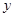 轴交于点
轴交于点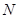 ,求点
,求点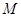 是椭圆
是椭圆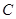 :
: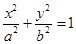
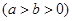 上一点,
上一点,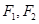 分别为
分别为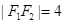 ,
,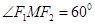 ,
,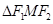 的面积为
的面积为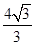 .
.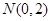 ,过点
,过点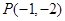 作直线
作直线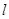 ,交椭圆
,交椭圆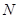 的
的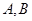 两点,直线
两点,直线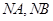 的斜率分别为
的斜率分别为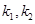 ,证明:
,证明: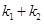 为定值.
为定值.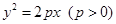 与直线
与直线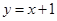 相切,
相切,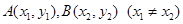 是抛物线上两个动点,
是抛物线上两个动点,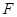 为抛物线的焦点,
为抛物线的焦点,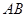 的垂直平分线
的垂直平分线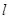 与
与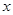 轴交于点
轴交于点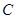 ,且
,且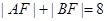 .
.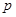 的值;
的值;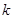 的取值范围.
的取值范围.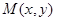 与定点
与定点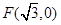 的距离和它到直线
的距离和它到直线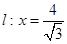 的距离之比是常数
的距离之比是常数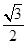 ,记点
,记点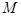 的轨迹为曲线
的轨迹为曲线 .
.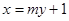 与曲线
与曲线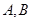 两点,
两点,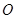 为坐标原点,求
为坐标原点,求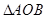 面积的最大值.
面积的最大值.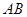 的两个端点在抛物线
的两个端点在抛物线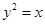 上滑动,则线段
上滑动,则线段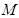 到
到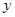 轴距离的最小值是
轴距离的最小值是 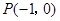 作曲线
作曲线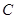 :
: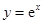 的切线,切点为
的切线,切点为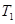 ,设
,设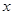 轴上的投影是点
轴上的投影是点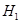 ,过点
,过点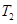 ,设
,设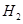 ,…,依次下去,得到第
,…,依次下去,得到第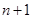
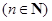 个切点
个切点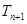 .则点
.则点