题目内容
已知函数 .
.
(1)判断函数 的奇偶性;(4分)
的奇偶性;(4分)
(2)若关于 的方程
的方程 有两解,求实数
有两解,求实数 的取值范围;(6分)
的取值范围;(6分)
(3)若 ,记
,记 ,试求函数
,试求函数 在区间
在区间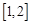 上的最大值.(10分)
上的最大值.(10分)
【答案】
(1)当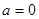 时,
时, 为偶函数;当
为偶函数;当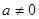 时,
时, 为非奇非偶函数。(4分)
为非奇非偶函数。(4分)
(2) ;(3)
;(3)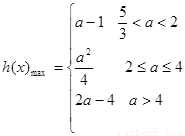
【解析】
试题分析:(1)当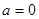 时,
时, 为偶函数;(3分)
为偶函数;(3分)
当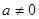 时,
时, 为非奇非偶函数。(4分)
为非奇非偶函数。(4分)
(2)由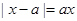 ,得
,得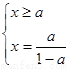 或
或 (6分)
(6分)
所以 则
则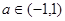 (10分)(用图象做给分)
(10分)(用图象做给分)
(3)
 (12分)
(12分)
当 时,
时, 在
在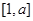 上递减,在[
上递减,在[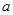 ,2]上递增,
,2]上递增,  ,
, 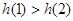 ,
, 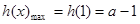 (15分)
(15分)
当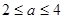 时,
时,  (17分)
(17分)
当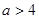 时,
时, 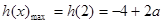 (19分)
(19分)
所以,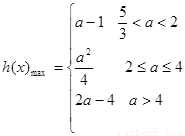 (20分)
(20分)
考点:本题考查了函数性质的运用及最值的求法
点评:函数的性质是高考考查的重点内容.根据函数单调性和奇偶性的定义,能判断函数的奇偶性,以及函数在某一区间的单调性,从数形结合的角度认识函数的单调性和奇偶性,掌握求函数最大值和最小值的常用方法.

练习册系列答案
相关题目

 (理)已知函数
(理)已知函数
 ,有h(h(a))=a;
,有h(h(a))=a;
 ,使得h(m)=m,若m是函数h(x)的中介元,记
,使得h(m)=m,若m是函数h(x)的中介元,记 时h(x)的中介元为xn,且
时h(x)的中介元为xn,且 ,若对任意的
,若对任意的 ,都有Sn<
,都有Sn<  ,求
,求 的取值范围;
的取值范围; 时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
 (理)已知函数
(理)已知函数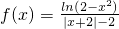 .
.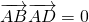 ,求D2+E2-4F的值;
,求D2+E2-4F的值; .
. ,求D2+E2-4F的值;
,求D2+E2-4F的值;
