题目内容
(本题12分)已知等比数列{an}的公比q=3,前3项和S3=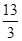 .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若函数f(x)=Asin(2x+φ)(A>0,0<φ<π)在x=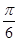 处取得最大值,且最大值为a3,
处取得最大值,且最大值为a3,
求函数f(x)的解析式.
【答案】
(1)an= ×3n-1=3n-2.(2)f(x)=3sin
×3n-1=3n-2.(2)f(x)=3sin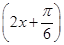 .
.
【解析】本试题主要是结合数列的概念得到数列的通项公式,然后结合三角函数中的性质得最值问题,从而求解得到解析式。
(1)利用等比数列{an}的公比q=3,前3项和S3=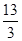 ,结合前n项和公式解得首项,从而得到通项公式
,结合前n项和公式解得首项,从而得到通项公式
(2)中利用第一问的结论,得到a3=3,从而得到函数的振幅,同时把x=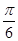 代入解析式中,是的函数取得最大值,得到φ的值,从而求解得到解析式。
代入解析式中,是的函数取得最大值,得到φ的值,从而求解得到解析式。
解:(Ⅰ)由q=3,S3=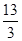 得
得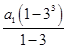 =
=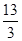 ,解得a1=
,解得a1= . 所以an=
. 所以an= ×3n-1=3n-2.
×3n-1=3n-2.
(Ⅱ)由(1)可知an=3n-2,所以a3=3. 因为函数f(x)的最大值为3,所以A=3;因为当x=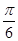 时f(x)取得最大值,所以sin
时f(x)取得最大值,所以sin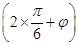 =1. 又0<φ<π,故φ=
=1. 又0<φ<π,故φ=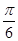 .
.
所以函数f(x)的解析式为f(x)=3sin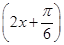 .
.

练习册系列答案
相关题目
 成等差数列.又数列
成等差数列.又数列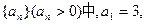 此数列的前n项的和Sn(
此数列的前n项的和Sn(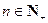 )对所有大于1的正整数n都有
)对所有大于1的正整数n都有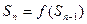 .
.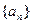 的第n+1项;
的第n+1项;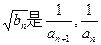 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。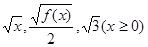 成等差数列.又数列
成等差数列.又数列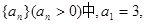 此数列的前n项的和Sn(
此数列的前n项的和Sn(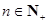 )对所有大于1的正整数n都有
)对所有大于1的正整数n都有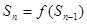 .
.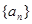 的第n+1项;
的第n+1项;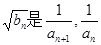 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn.