题目内容
在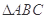 中,
中,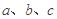 分别为内角
分别为内角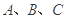 所对的边,且
所对的边,且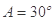 .现给出三个条件:①
.现给出三个条件:①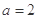 ; ②
; ②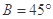 ;③
;③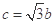 .试从中选出两个可以确定
.试从中选出两个可以确定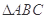 的条件,并以此为依据求
的条件,并以此为依据求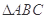 的面积.(只需写出一个选定方案即可)你选择的条件是 (用序号填写);由此得到的
的面积.(只需写出一个选定方案即可)你选择的条件是 (用序号填写);由此得到的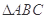 的面积为 .
的面积为 .
【答案】
①②,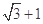 (或①③,
(或①③, )
)
【解析】
试题分析:在三角形ABC中
∵A=30,a=2,B=45°,由正弦定理知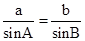 ,
,
∴b=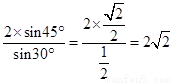 ,
,
C=180°-45°-30°=105°,
∴△ABC的面积为 absinC=
absinC= ×2×
×2×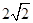 ×sin105°=
×sin105°=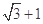 ,
,
故答案为①②,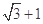 。
。
考点:本题主要考查正弦定理的应用,三角形面积计算。
点评:典型题,对于三角形中所给的条件角A,选择边a和角B,是一个比较容易计算的问题,只要应用正弦定理求出边的长,根据三角形内角和求出角的大小,就可以用正弦定理表示出面积。

练习册系列答案
相关题目
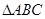 中,
中,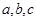 分别为内角
分别为内角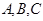 所对的边,且满足
所对的边,且满足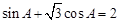 .
.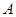 的大小;
的大小;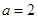 ; ②
; ②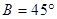 ;③
;③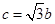 .
.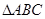 中,
中, 分别为内角
分别为内角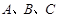 所对的边,且
所对的边,且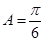 .现给出三个条件:①
.现给出三个条件:①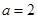 ; ②
; ②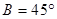 ;③
;③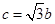 .试从中选出两个可以确定
.试从中选出两个可以确定 中,
中, 分别为内角
分别为内角 所对的边,且
所对的边,且 .
. ; ②
; ②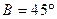 ;③
;③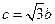 .试从中选出两个可以确定
.试从中选出两个可以确定