题目内容
已知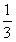 ≤a≤1,若函数f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a)。
≤a≤1,若函数f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a)。
(1)求g(a)的函数表达式;
(2)判断函数g(a)在区间[ ,1]上的单调性,并求出g(a)的最小值。
,1]上的单调性,并求出g(a)的最小值。
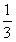 ≤a≤1,若函数f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a)。
≤a≤1,若函数f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a)。(1)求g(a)的函数表达式;
(2)判断函数g(a)在区间[
 ,1]上的单调性,并求出g(a)的最小值。
,1]上的单调性,并求出g(a)的最小值。 解:(1)∵ ≤a≤1,
≤a≤1,
∴f(x)的图像为开口向上的抛物线,且对称轴为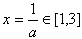 ,
,
∴f(x)有最小值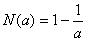 ,
,
当2≤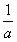 ≤3时,
≤3时,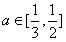 ,f(x)有最大值M(a)=f(1)=a-1;
,f(x)有最大值M(a)=f(1)=a-1;
当1≤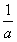 <2时,
<2时, ,f(x)有最大值M(a)=f(3)=9a-5;
,f(x)有最大值M(a)=f(3)=9a-5;
∴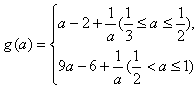 。
。
(2)设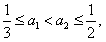
则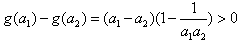 ,∴
,∴ ,
,
∴g(a)在 上是减函数;
上是减函数;
设
则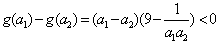 ,
,
∴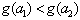 ,
,
∴ 在
在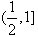 上是增函数,
上是增函数,
∴当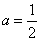 时,g(a)有最小值
时,g(a)有最小值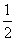 。
。
 ≤a≤1,
≤a≤1,∴f(x)的图像为开口向上的抛物线,且对称轴为
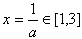 ,
,∴f(x)有最小值
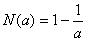 ,
,当2≤
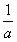 ≤3时,
≤3时,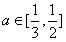 ,f(x)有最大值M(a)=f(1)=a-1;
,f(x)有最大值M(a)=f(1)=a-1;当1≤
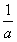 <2时,
<2时, ,f(x)有最大值M(a)=f(3)=9a-5;
,f(x)有最大值M(a)=f(3)=9a-5;∴
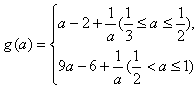 。
。 (2)设
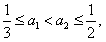
则
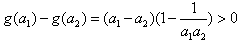 ,∴
,∴ ,
,∴g(a)在
 上是减函数;
上是减函数;设

则
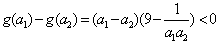 ,
,∴
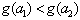 ,
,∴
 在
在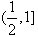 上是增函数,
上是增函数,∴当
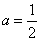 时,g(a)有最小值
时,g(a)有最小值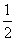 。
。
练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目