题目内容

（2012•湘潭三模）若
x-y≤0
x+y≥0
y≤a
，若z=x+2y的最大值为3，则a的值是（　　）
分析：作出不等式表示的平面区域，明确目标函数的几何意义，根据z=x+2y的最大值为3，即可求a的值．
解答：解：作出不等式表示的平面区域，如图

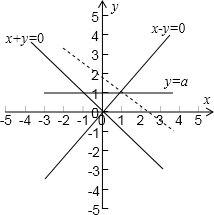
z=x+2y的几何意义是直线y=-
1
2
x+
z
2
纵截距的一半
由
x-y=0
y=a
，可得x=y=a，根据图形可知在（a，a）处，z=x+2y的最大值为3
∴a+2a=3
∴a=1
故选A．
点评：本题考查线性规划知识，考查求函数的最值，正确作出不等式表示的平面区域，明确目标函数的几何意义是关键．
练习册系列答案
相关题目
（2012•湘潭三模）已知抛物线y2=2px（p＞0）的准线与圆（x-3）2+y2=16相切，则p的值为
2
2
．
（2012•湘潭三模）已知函数f(x)=(m+
1
m
)lnx+
1
x
-x，（其中常数m＞0）
（1）当m=2时，求f（x）的极大值；
（2）试讨论f（x）在区间（0，1）上的单调性；
（3）当m∈[3，+∞）时，曲线y=f（x）上总存在相异两点P（x1，f（x1））、Q（x2，f（x2）），使得曲线y=f（x）在点P、Q处的切线互相平行，求x1+x2的取值范围．
（2012•湘潭三模）已知复数z=
2i
1-i
，则复数z为（　　）
（2012•湘潭三模）“x＞1”是“x2-2x+1＞0”的（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网