题目内容
在递减等比数列{an}中,a1+a6=33,a3·a4=32.设Tn=lga1+lga2+…+lgan,求使Tn＞0的n的最大取值.
解：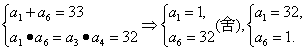
∴q=
.
∴an=32(
)n-1=26-n.
∴Tn=lga1a2…an=lg25·24…26-n=［5+4+…+(6-n)］·lg2
=
·lg2＞0. ∴n的最大值为10.
练习册系列答案
相关题目
题目内容
在递减等比数列{an}中,a1+a6=33,a3·a4=32.设Tn=lga1+lga2+…+lgan,求使Tn＞0的n的最大取值.
解：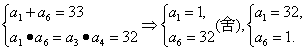
∴q=.
∴an=32()n-1=26-n.
∴Tn=lga1a2…an=lg25·24…26-n=［5+4+…+(6-n)］·lg2
=·lg2＞0. ∴n的最大值为10.