题目内容
计算| 1 |
| 3•1! |
| 1 |
| 4•2! |
| 1 |
| 5•3! |
| 1 |
| (n+2)n! |
分析:根据题意得通项公式,分子分母同乘(n+1)!,再把an拆成两项相减,然后再求和.
解答:解:由题意得,数列的通项公式
an=
=
=
-
,
∴
+
+
+…+
=(1-
)+(
-
)+(
-
)+…+[
-
]+[
-
]
=1+
-
-
=
-
an=
| 1 |
| (n+2)n! |
| (n+1)! |
| n!(n+2)! |
| 1 |
| n! |
| 1 |
| (n+2)! |
∴
| 1 |
| 3•1! |
| 1 |
| 4•2! |
| 1 |
| 5•3! |
| 1 |
| (n+2)n! |
=(1-
| 1 |
| 3! |
| 1 |
| 2! |
| 1 |
| 4! |
| 1 |
| 3! |
| 1 |
| 5! |
| 1 |
| (n-1)! |
| 1 |
| (n+1)! |
| 1 |
| n! |
| 1 |
| (n+2)! |
=1+
| 1 |
| 2! |
| 1 |
| (n+1)! |
| 1 |
| (n+2)! |
=
| 3 |
| 2 |
| n+3 |
| (n+2)! |
点评:本题用了裂项相消法求和,通项中含有阶乘时通常分子分母同乘另一个阶乘后再裂项,求和时消不去的项是前后对称的.

练习册系列答案
相关题目
(本小题满分12分)
 某班甲、乙两名同学参加l00米达标训练,在相同条件下两人l0次训练的成绩(单位:秒)如下:
某班甲、乙两名同学参加l00米达标训练,在相同条件下两人l0次训练的成绩(单位:秒)如下:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
甲 |
11.6 |
12.2 |
13.2 |
13.9 |
14.0 |
11.5 |
13.1 |
14.5 |
11.7 |
14.3 |
|
乙 |
12.3 |
13.3 |
14.3 |
11.7 |
12.0 |
12.8 |
13.2 |
13.8 |
14.1 |
12.5 |
(I)请作出样本数据的茎叶图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论).
(Ⅱ)从甲、乙两人的10次训练成绩中各随机抽取一次,求抽取的成绩中至少有一个比12.8秒差的概率.
(Ⅲ)经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]
之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.
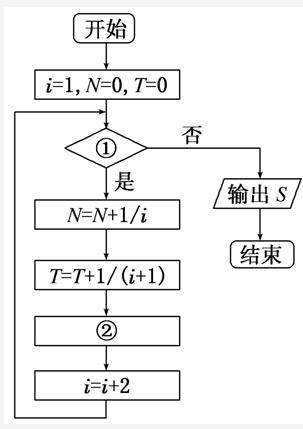 如图给出的是计算S=1-
如图给出的是计算S=1-