题目内容
已知函数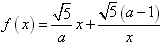 ,(x≠0)(a≠0),
,(x≠0)(a≠0),
(1)试就实数a的不同取值,写出该函数的单调递增区间;
(2)已知当a>0时,函数在(0,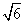 )上单调递减,在(
)上单调递减,在(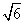 ,+∞)上单调递增,求a的值并写出函数的解析式;
,+∞)上单调递增,求a的值并写出函数的解析式;
(3)若函数f(x)在区间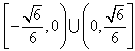 内有反函数,试求出实数a的取值范围。
内有反函数,试求出实数a的取值范围。
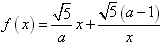 ,(x≠0)(a≠0),
,(x≠0)(a≠0),(1)试就实数a的不同取值,写出该函数的单调递增区间;
(2)已知当a>0时,函数在(0,
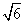 )上单调递减,在(
)上单调递减,在(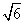 ,+∞)上单调递增,求a的值并写出函数的解析式;
,+∞)上单调递增,求a的值并写出函数的解析式;(3)若函数f(x)在区间
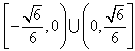 内有反函数,试求出实数a的取值范围。
内有反函数,试求出实数a的取值范围。 解:(1)①当a<0时,函数f(x)的单调递增区间为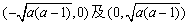 ;
;
②当0<a≤1时,函数f(x)的单调递增区间为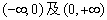 ;
;
③当a>1时,函数f(x)的单调递增区间为 。
。
(2)由题设及(1)中③知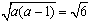 ,且a>1,解得a=3,
,且a>1,解得a=3,
因此函数解析式为 ;
;
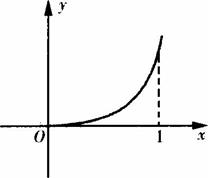
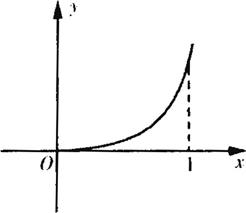
(3)1#当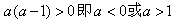 时,
时,
由图象知 ,解得
,解得 ;
;
2#当a=1时,函数为正比例函数,故在区间内存在反函数,所以a=1成立;
3#当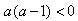 ,得到
,得到 ;
;
综上,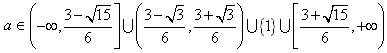 。
。
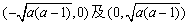 ;
;②当0<a≤1时,函数f(x)的单调递增区间为
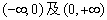 ;
;③当a>1时,函数f(x)的单调递增区间为
 。
。(2)由题设及(1)中③知
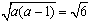 ,且a>1,解得a=3,
,且a>1,解得a=3, 因此函数解析式为
 ;
;(3)1#当
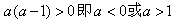 时,
时,由图象知
 ,解得
,解得 ;
;2#当a=1时,函数为正比例函数,故在区间内存在反函数,所以a=1成立;
3#当
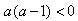 ,得到
,得到 ;
;综上,
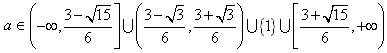 。
。
练习册系列答案
相关题目
已知函数,f(x)=
,则复合函数f{f[f(-1)]}=( )
|
| A、x2+1 |
| B、π2+1 |
| C、-π |
| D、0 |