题目内容
一个空间几何体的正视图、侧视图是两个边长为1的正方形，俯视图是直角边长为1的等腰直角三角形，则这个几何体的体积等于( )
| A．1 | B． | C． | D． |
B
解析考点：由三视图求面积、体积．
分析：判断三视图复原的几何体的形状，通过已知的三视图的数据，求出几何体的体积
解：由题意可知三视图复原的几何体是一个直放的三棱柱，
三棱柱的底面是边长为1的等腰直角三角形，高为1的三棱柱．
所以几何体的体积为：×1×1×1=．
故选B．
练习册系列答案
科学实验活动册系列答案
相关题目
的侧棱与底面边长都相等，
在底面
内的射影为
的中心，则
与底面
一个空间几何体的三视图如图所示，则该几何体的的体积为
A． |
B． |
C． |
D． |
对于四面体ABCD，给出下列四个命题：
①若AB=AC，BD=CD，则BC⊥AD； ②若AB=CD，AC=BD，则BC⊥AD；
③若AB⊥AC，BD⊥CD，则BC⊥AD；④若AB⊥CD，AC⊥BD，则BC⊥AD；
其中正确的命题的序号是( )
| A．①② | B．②③ | C．②④ | D．①④ |
右图是一个几何体的平面展开图，其中ABCD为
正方形，E、F分别为PA、PD的中点，在此几何体中，
给出下面四个结论：
①直线BE与直线CF异面；②直线BE与直线AF异面；
③直线EF//平面PBC； ④平面BCE⊥平面PAD.
其中正确结论的个数是
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其侧视图的面积为 （ ）
| A．4 | B． | C． | D．2 |
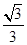
，其底面是边长为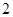
的正六边形，侧棱长都相等，则该六棱锥的侧面积为 .