Question

P₁是椭圆+y²=1(a＞0且a≠1)上不与顶点重合的任一点,P₁P₂是垂直于x轴的弦,A₁(-a,0),A₂(a,0)是椭圆的两个顶点,直线A₁P₁与直线A₂P₂的交点为P.

(1)求点P的轨迹曲线C的方程;

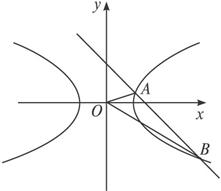
(2)设曲线C与直线l:x+y=1相交于两个不同的点A、B,求曲线C的离心率e的取值范围;

(3)设曲线C与直线l:x+y=1相交于两个不同的点A、B,O为坐标原点,且=-3,求a的值.

(文)(本小题满分12分)设函数f(x)=x³+2ax²-3a²x+a(0＜a＜1).

(1)求函数f(x)的单调区间;

(2)若当x∈［a,2］时,恒有f(x)≤0,试确定实数a的取值范围.

Answer 1

(理)解析：(1)设P₁(m,n)(mn≠0),则P₂(m,-n),直线A₁P₁:y=(x+a);①

直线A₂P₂:y=(x-a);②                                                   

设P点坐标为(x,y),

由①②得m=,n=,                                                      

       

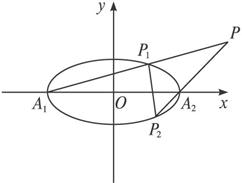
∵点P₁(m,n)在椭圆+y²=1上,

∴有m²+a²n²=a²,

即()²+a²()²=a²,整理得-y²=1(y≠0),

∴直线A₁P₁与直线A₂P₂交点P的轨迹方程是双曲线-y²=1(y≠0).                

(2)由C与l相交于两个不同的点,故知方程组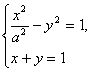有两个不同的实数解.消去y并整理得(1-a²)x²+2a²x-2a²=0.

又∵a＞0且a≠1,

∴4a⁴+8a²(1-a²)＞0.

∴0＜a²＜2且a²≠1.                                                         

双曲线的离心率e=.

∴＜e＜或e＞,即e∈()∪(,+∞).                        

(3)设A(x₁,y₁)、B(x₂,y₂),

则-3=

=x₁x₂+y₁y₂

=x₁x₂+(1-x₁)(1-x₂)

=2x₁x₂-(x₁+x₂)+1

=+1,

即=-4,由a＞0,得a=.                                               

(文)解：(1)∵f(x)=x³+2ax²-3a²x+a(0＜a＜1),

∴f′(x)=-x²+4ax-3a²=-(x-a)(x-3a).                                              

∵0＜a＜1,∴f′(x)＞0a＜x＜3a,f′(x)＜0x＜a或x＞3a.                      

∴函数f(x)的递增区间为［a,3a］;递减区间为(-∞,a］,［3a,+∞).                   

(2)∵x∈［a,2］,

①当2≤3a,即≤a＜1时,f(x)在区间［a,2］内是增函数.

∴f(x)_max=f(2)=a-6a².

又当x∈［a,2］时,恒有f(x)≤0,

∴.                                       

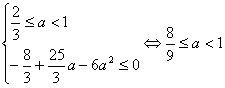②当2＞3a即0＜a＜时,则f(x)在［a,3a］上单调递增;在［3a,2］上单调递减,

∴f(x)_max=f(3a)=a.

又当x∈［a,2］时,恒有f(x)≤0,

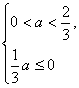∴(无解).

综上所述,a的取值范围是≤a＜1.