题目内容
已知函数f(x)=(1)判断函数f(x)在区间(0,+∞)上的单调性,证明你的结论;
(2)若当x>0时,f(x)>![]() 恒成立,求正整数k的最大值.(参考数据:ln2≈0.7,ln3≈1.1)
恒成立,求正整数k的最大值.(参考数据:ln2≈0.7,ln3≈1.1)
(文) P1是椭圆![]() +y2=1(a>0且a≠1)上不与顶点重合的任一点,P1P2是垂直于x轴的弦,A1(-a,0),A2(a,0)是椭圆的两个端点,直线A1P1与直线A2P2交点为P.
+y2=1(a>0且a≠1)上不与顶点重合的任一点,P1P2是垂直于x轴的弦,A1(-a,0),A2(a,0)是椭圆的两个端点,直线A1P1与直线A2P2交点为P.
(1)求P点的轨迹曲线C的方程;
(2)设曲线C与直线l:x+y=1相交于两个不同的点A、B,求曲线C的离心率e的取值范围;
(3)设曲线C与直线l:x+y=1相交于两个不同的点A、B,O为坐标原点,且![]() =-3,求a的值.
=-3,求a的值.
(理)解:(1)f′(x)=![]() [
[![]() -1-ln(x+1)]=
-1-ln(x+1)]=![]() [
[![]() +ln(x+1)],
+ln(x+1)],
∵x>0,∴x2>0,![]() >0,ln(x+1)>0.
>0,ln(x+1)>0.
∴f′(x)<0.
因此函数f(x)在区间(0,+∞)上是减函数.
(2)(方法1)当x>0时,f(x)>![]() 恒成立,令x=1有k<2(1+ln2).又k为正整数,
恒成立,令x=1有k<2(1+ln2).又k为正整数,
∴k的最大值不大于3.
下面证明当k=3时,f(x)>![]() (x>0)恒成立,
(x>0)恒成立,
即证当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
令g(x)=(x+1)ln(x+1)+1-2x,则g′(x)=ln(x+1)-1,
当x>e-1时,g′(x)>0;当0<x<e-1时,g′(x)<0.
∴当x=e-1时,g(x)取得最小值g(e-1)=3-e>0.
∴当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
因此正整数k的最大值为3.
(方法2)当x>0,f(x)>![]() 恒成立.
恒成立.
h(x)=![]() >k对x>0恒成立.h(x)(x>0)的最小值大于k.
>k对x>0恒成立.h(x)(x>0)的最小值大于k.
h′(x)=![]() ,记φ(x)=x-1-ln(x+1)(x>0),
,记φ(x)=x-1-ln(x+1)(x>0),
则φ′(x)=![]() >0,
>0,
∴φ(x)在(0,+∞)上连续递增.
又φ(2)=1-ln3<0,φ(3)=2-2ln2>0,
∴φ(x)=0存在唯一实根a,且满足:a∈(2,3),即a-1-ln(a+1)=0.∴a=1+ln(a+1).
由x>a时,φ(x)>0,h′(x)>0;0<x<a时,φ(x)<0,h′(x)<0知:
h(x)(x>0)的最小值为h(a)=![]() =a+1.
=a+1.
又2<a<3,∴3<a+1<4,为使k<h(x)对于x>0恒成立,
因此正整数k的最大值为3.
(文)(1)解:设P1(m,n)(mn≠0),则P2(m,-n),
直线A1P1:y=![]() (x+a);①
(x+a);①
直线A2P2:y=![]() (x-a);②
(x-a);②
设P点坐标为(x,y),
由①②得m=![]() ,n=
,n=![]() ,
,
∵点P1(m,n)在椭圆![]() +y2=1上,
+y2=1上,
∴有m2+a2n2=a2,
即(![]() )2+a2(
)2+a2(![]() )2=a2,整理得
)2=a2,整理得![]() -y2=1(y≠0).
-y2=1(y≠0).
∴直线A1P1与直线A2P2交点P的轨迹方程是双曲线![]() -y2=1(y≠0).
-y2=1(y≠0).
(2)由C与l相交于两个不同的点,故知方程组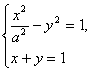 有两个不同的实数解.消去y并整理得(1-a2)x2+2a2x-2a2=0.
有两个不同的实数解.消去y并整理得(1-a2)x2+2a2x-2a2=0.
又∵a>0且a≠1,
∴4a4+8a2(1-a2)>0.
∴0<a2<2且a2≠1.
双曲线的离心率e=![]() .
.
∴![]() <e<
<e<![]() 或e>
或e>![]() ,即e∈(
,即e∈(![]() )∪(
)∪(![]() ,+∞).
,+∞).
(3)设A(x1,y1)、B(x2,y2),
则-3=![]() =x1x2+y1y2=x1x2+(1-x1)(1-x2)=2x1x2-(x1+x2)+1=
=x1x2+y1y2=x1x2+(1-x1)(1-x2)=2x1x2-(x1+x2)+1=![]() +1,
+1,
即![]() =-4,由a>0,得a=
=-4,由a>0,得a=![]() .
.

 期末集结号系列答案
期末集结号系列答案 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|