题目内容
22.设椭圆(Ⅰ)求实数m的取值范围;
(Ⅱ)设L是相应于焦点F2的准线,直线PF2与L相交于点Q.若![]() =
=
2-![]() .求直线PF2的方程.
.求直线PF2的方程.
22. 本小题主要考查直线和椭圆的基本知识,以及综合分析和解题能力.
解:(Ⅰ)由题设有m>0,c=![]() ,
,
设点P的坐标为(x0,y0),由PF1⊥PF2,得![]() =-1,
=-1,
化简得x02+y![]() =m. ①
=m. ①
将①与![]() +y02=1联立,解得x02=
+y02=1联立,解得x02=![]() ,y02=
,y02=![]() .
.
由m>0,x02=![]() ≥0,得m≥1.
≥0,得m≥1.
所以m的取值范围是m≥1.
(Ⅱ)准线L的方程为x=![]() .设点Q的坐标为(x1,y1),则
.设点Q的坐标为(x1,y1),则
x1=![]() .
.
![]() =
=![]() =
=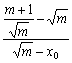 . ②
. ②
将x0=![]() 代入②,化简得
代入②,化简得
![]() =
=![]() =m+
=m+![]() .
.
由题设![]() =2-
=2-![]() ,得m+
,得m+![]() =2-
=2-![]() ,无解.
,无解.
将x0=-![]() 代入②,化简得
代入②,化简得
![]() =
=![]() =m-
=m-![]() .
.
由题设![]() =2-
=2-![]() ,得m-
,得m-![]() =2-
=2-![]() .
.
解得m=2.
从而x0=-![]() ,y0=±
,y0=±![]() ,c=
,c=![]() ,得PF2的方程
,得PF2的方程
y=±(![]() -2)(x-
-2)(x-![]() ).
).

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目