题目内容
圆心在y轴的正半轴上，过椭圆
+
=1的右焦点且与其右准线相切的圆的方程为 ．
| x2 |
| 5 |
| y2 |
| 4 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：首先求出椭圆的右焦点和右准线，由题意设出圆的方程求参数a，r．
解答：
解：由题意，设圆心为（0，a），半径为r，则x2+（y-a）2=r2，
因为圆过椭圆
+
=1的右焦点且与其右准线相切，并且椭圆
+
=1的右焦点为（1，0），其右准线为：x=5
所以1+a2=52，所以a=2
，
所以圆的方程为：x2+（y-2
）2=25；
故答案为：x2+（y-2
）2=25．
因为圆过椭圆
| x2 |
| 5 |
| y2 |
| 4 |
| x2 |
| 5 |
| y2 |
| 4 |
所以1+a2=52，所以a=2
| 6 |
所以圆的方程为：x2+（y-2
| 6 |
故答案为：x2+（y-2
| 6 |
点评：本题考查了椭圆的性质以及圆的方程求法，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
在等差数列{an}中，a5=33，公差d=3，则201是该数列的第（ ）项．
| A、60 | B、61 | C、62 | D、63 |
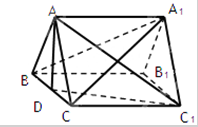如图所示，在三棱柱ABC-A1B1C1中，底面ABC是边长为2的正三角形，侧棱长为3，且侧棱AA1⊥面ABC，点D是BC的中点，求证：平面BB1C1C丄平面ADC1．