题目内容
已知:三次函数f(x)=x3+ax2+bx+c,在(-∞,-1),(2+∞)上单调增,在(-1,2)上单调减,当且仅当x>4时,f(x)>x2-4x+5
(1)求函数f(x)的解析式;
(2)若函数![]() ,求h(x)的单调区间.
,求h(x)的单调区间.
答案:
解析:
解析:
|
解:(1) 令 故 故 (2) 当m≤-2时,-m≥2,定义域: 当-2<m≤-1时,2>-m≥1,定义域:(-m,2)∪(2,+∞) 当m>-1时,-m<1,定义域:(-m,2)∪(2,+∞) 由 故在(1,2),(2,+∞)上单增;在 所以当m≤-2时,h(x)在(-m,+∞)上单增; 当 当m>-1时,在(1,2),(2,+∞)上单增;在(-m,1)单减 14分 |

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 4分
4分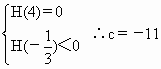
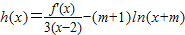 ,求h(x)的单调区间.
,求h(x)的单调区间.