题目内容
已知:三次函数f(x)=x3+ax2+bx+c,在(-∞,-1),(2,+∞)上单调增,在(-1,2)上单调减,当且仅当x>4时,f(x)>x2-4x+5=g(x).
(1)求函数f(x)的解析式;
(2)若函数y=m与函数f(x)、g(x)的图象共有3个交点,求m的取值范围.
答案:
解析:
解析:
|
解:(1) 令 故 故 (2)因 同理f(2)=-21 ∴当 又 故当m>1时,直线 故m的取值范围: |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
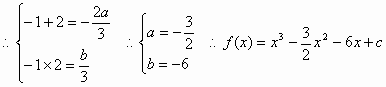 4分
4分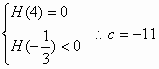
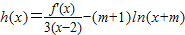 ,求h(x)的单调区间.
,求h(x)的单调区间.