题目内容
(本小题12分)设函数 ,
, ,其中
,其中 ,将
,将 的最小值记为
的最小值记为 .
.
(I)求 的表达式;
的表达式;
(II)设 ,讨论
,讨论 在区间
在区间 内的单调性.
内的单调性.
 ,
, ,其中
,其中 ,将
,将 的最小值记为
的最小值记为 .
.(I)求
 的表达式;
的表达式;(II)设
 ,讨论
,讨论 在区间
在区间 内的单调性.
内的单调性.(I)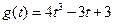
(II)当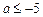 时,
时,  在区间
在区间 内单调递增;
内单调递增;
当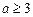 时,
时,  在区间
在区间 内单调递减;
内单调递减;
当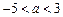 时,
时,  在区间
在区间 单调递减,在区间
单调递减,在区间 单调递增.
单调递增.
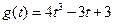
(II)当
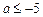 时,
时,  在区间
在区间 内单调递增;
内单调递增;当
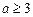 时,
时,  在区间
在区间 内单调递减;
内单调递减;当
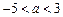 时,
时,  在区间
在区间 单调递减,在区间
单调递减,在区间 单调递增.
单调递增.解:(I)
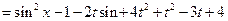
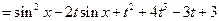
 .
.
由于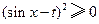 ,
, ,故当
,故当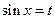 时,
时, 达到其最小值
达到其最小值 ,即
,即
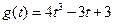 .
.
(II)

令 ,得
,得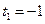 (舍去),
(舍去),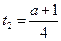
当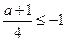 ,即
,即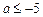 时,
时,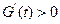 ,
, 在区间
在区间 内单调递增
内单调递增
当 ,即
,即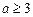 时,
时,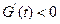 ,
, 在区间
在区间 内单调递减
内单调递减
当 ,即
,即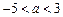 时,当
时,当 时
时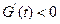 ,
,
当 时
时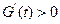 ,即
,即 在区间
在区间 单调递减,在区间
单调递减,在区间 单调递增
单调递增
综上,当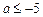 时,
时,  在区间
在区间 内单调递增;
内单调递增;
当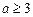 时,
时,  在区间
在区间 内单调递减;
内单调递减;
当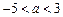 时,
时,  在区间
在区间 单调递减,在区间
单调递减,在区间 单调递增.
单调递增.

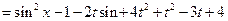
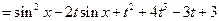
 .
.由于
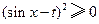 ,
, ,故当
,故当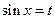 时,
时, 达到其最小值
达到其最小值 ,即
,即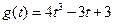 .
.(II)


令
 ,得
,得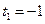 (舍去),
(舍去),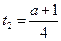
当
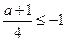 ,即
,即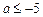 时,
时,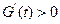 ,
, 在区间
在区间 内单调递增
内单调递增当
 ,即
,即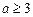 时,
时,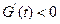 ,
, 在区间
在区间 内单调递减
内单调递减当
 ,即
,即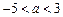 时,当
时,当 时
时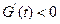 ,
,当
 时
时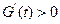 ,即
,即 在区间
在区间 单调递减,在区间
单调递减,在区间 单调递增
单调递增综上,当
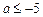 时,
时,  在区间
在区间 内单调递增;
内单调递增;当
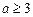 时,
时,  在区间
在区间 内单调递减;
内单调递减;当
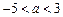 时,
时,  在区间
在区间 单调递减,在区间
单调递减,在区间 单调递增.
单调递增.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
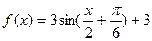
 出
出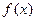 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴; 可由
可由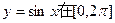 上的图象经怎样的变换得到
上的图象经怎样的变换得到 ,
, ),
), =(
=(
 ,
, ),x
),x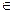 R求:
R求: 的解析式并进行化简;
的解析式并进行化简; 的方程
的方程 在
在 上有解,求实数
上有解,求实数 的取值范围。
的取值范围。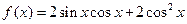 (
(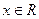 ).
).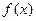 的最小正周期,并求
的最小正周期,并求 ,若
,若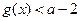 对于
对于 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.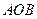 中,
中,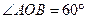 ,
,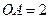 ,在弧
,在弧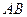 上有一动点
上有一动点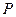 ,过
,过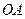 于
于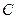 ,设
,设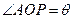 ,
,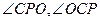 及OC的长(可用
及OC的长(可用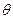 表示);
表示);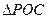 面积的最大值及此时
面积的最大值及此时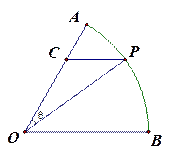
 的值为 ( )
的值为 ( )





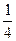


 ( )
( )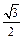



 ( )
( )


