题目内容
已知直线l：y=x+m，m∈R．
(1)若以点M（2，0）为圆心的圆与直线l相切与点P，且点P在y轴上，求该圆的方程；
(2)若直线l关于x轴对称的直线为lˊ，问直线lˊ与抛物线C：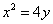
是否相切？说明理由．
(1)若以点M（2，0）为圆心的圆与直线l相切与点P，且点P在y轴上，求该圆的方程；
(2)若直线l关于x轴对称的直线为lˊ，问直线lˊ与抛物线C：
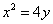是否相切？说明理由．(1)
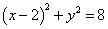
(2)见解析；
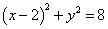
(2)见解析；
（1）依题意，点P的坐标为（0，m）
因为圆与直线l相切与点P，∴MP⊥l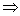
，
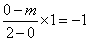解得m=2，即点P的坐标为（0，2）
从而圆的半径r=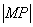
=
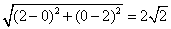
故所求圆的方程为；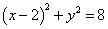
（2）因为直线l的方程为y=x+m，
所以直线lˊ的方程为y=－x－m代入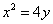得
∵
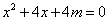
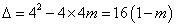∴m=1时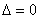
，即直线lˊ与抛物线C相切
当m≠1时，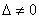
，即直线lˊ与抛物线C不相切
综上，当m=1时，直线lˊ与抛物线C相切；
当m≠1时，直线lˊ与抛物线C不相切．
因为圆与直线l相切与点P，∴MP⊥l
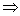
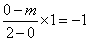，解得m=2，即点P的坐标为（0，2）
从而圆的半径r=
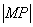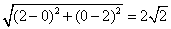
=故所求圆的方程为
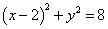；（2）因为直线l的方程为y=x+m，
所以直线lˊ的方程为y=－x－m代入
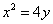得∵
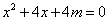
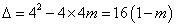∴m=1时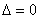，即直线lˊ与抛物线C相切当m≠1时，
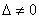，即直线lˊ与抛物线C不相切综上，当m=1时，直线lˊ与抛物线C相切；
当m≠1时，直线lˊ与抛物线C不相切．
练习册系列答案
阅读快车系列答案
相关题目
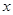轴正半轴为极轴，已知点P的直角坐标为(1,-5),点C的极坐标为
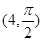,若直线l经过点P,且倾斜角为
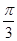，圆C的半径为4.
是直线
上一动点，
是圆C：
的两条切线，A、B是切点，若四边形
的最小面积是2，则
的值为？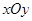
中，圆C的方程为
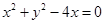．若直线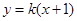
上存在一点
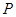，使过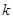
的取值范围是 ．
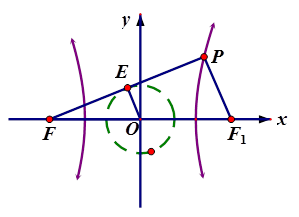
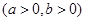的左焦点
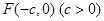，作圆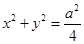
的切线，切点为
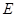，延长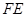
交双曲线右支于点
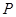，若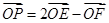
，则双曲线的离心率为（ ）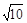 
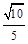
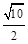
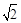
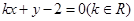与圆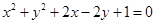
的位置关系是
值有关
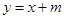与曲线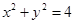
交于不同的两点
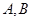，若
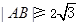，则实数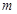
的取值范围是 .