题目内容
一个正三棱锥的侧棱长为1,底边长为| 2 |
分析:由题意球心到正三棱锥四个顶点的距离相等都为R,由于顶点在底面的射影是底面的中心,故棱锥的高易求出,由此球心到底面的距离可以表示出,故可以利用球心到谋面的距离、球的半径、底面中心到顶点的距离这个直角三角形利用勾股定理建立方程求出球的半径.
解答:解:由题意设球的半径为R,正三棱锥在底面的投影是底面的中心,
由于一个正三棱锥的侧棱长为1,底边长为
,故底面三角形的高为
,底面中心到底面三角形的顶点的距离是
×
=
故三棱锥的顶点到底面的距离是
=
故球心到底面的距离是
-R,由几何体的结构知(
)2+(
-R)2=R2得R=
此球的表面积为4×π×(
)2=3π
故答案为3π
由于一个正三棱锥的侧棱长为1,底边长为
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
故三棱锥的顶点到底面的距离是
12-(
|
| ||
| 3 |
故球心到底面的距离是
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 2 |
此球的表面积为4×π×(
| ||
| 2 |
故答案为3π
点评:本题考查球的体积和表面积,求解本题的关键是根据三棱锥的几何结构求出球的半径,再由公式求表面积.对几何体空间结构的透彻了解,是解立体几何体的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
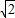 ,四个顶点在同一球面上,则此球的表面积为 .
,四个顶点在同一球面上,则此球的表面积为 .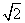 ,四个顶点在同一球面上,则此球的表面积为( )。
,四个顶点在同一球面上,则此球的表面积为( )。