题目内容
一个正三棱锥的侧棱长为1,底边长为
,四个顶点在同一球面上,则此球的表面积为______.
| 2 |
由题意设球的半径为R,正三棱锥在底面的投影是底面的中心,
由于一个正三棱锥的侧棱长为1,底边长为
,故底面三角形的高为
,底面中心到底面三角形的顶点的距离是
×
=
故三棱锥的顶点到底面的距离是
=
故球心到底面的距离是
-R,由几何体的结构知(
)2+(
-R)2=R2得R=
此球的表面积为4×π×(
)2=3π
故答案为3π
由于一个正三棱锥的侧棱长为1,底边长为
| 2 |
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
故三棱锥的顶点到底面的距离是
12-(
|
| ||
| 3 |
故球心到底面的距离是
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 2 |
此球的表面积为4×π×(
| ||
| 2 |
故答案为3π

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
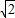 ,四个顶点在同一球面上,则此球的表面积为 .
,四个顶点在同一球面上,则此球的表面积为 .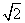 ,四个顶点在同一球面上,则此球的表面积为( )。
,四个顶点在同一球面上,则此球的表面积为( )。