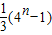题目内容
数列{an},已知对任意正整数n,a1+a2+a3+…+an=2n-1,则a12+a22+a32+…+an2 等于( )
| A、(2n-1)2 | ||
B、
| ||
C、
| ||
| D、4n-1 |
分析:首先根据a1+a2+a3+…+an=2n-1,求出a1+a2+a3+…+an-1=2n-1-1,两式相减即可求出数列{an}的关系式,然后求出数列{an2}的递推式,最后根据等比数列求和公式进行解答.
解答:解:∵a1+a2+a3+…+an=2n-1…①
∴a1+a2+a3+…+an-1=2n-1-1…②,
①-②得an=2n-1,
∴an2=22n-2,
∴数列{an2}是以1为首项,4为公比的等比数列,
∴a12+a22+a32+…+an2=
=
(4n-1),
故选C.
∴a1+a2+a3+…+an-1=2n-1-1…②,
①-②得an=2n-1,
∴an2=22n-2,
∴数列{an2}是以1为首项,4为公比的等比数列,
∴a12+a22+a32+…+an2=
| 1-4n |
| 1-4 |
| 1 |
| 3 |
故选C.
点评:本题主要考查数列求和和求数列递推式的知识点,解答本题的关键是求出数列{an}的通项公式,本题难度一般.

练习册系列答案
相关题目