题目内容
设复数z同时满足下列条件：
(1)复数z在复平面内对应的点位于第二象限；(2)z
＋2i＝8＋ai(a∈R)，试求a的取值范围．
(1)复数z在复平面内对应的点位于第二象限；(2)z
＋2i＝8＋ai(a∈R)，试求a的取值范围．[－6,0)
设z＝x＋yi，则由条件(1)知x＜0，y＞0.
又z＋2i＝8＋ai，故
(x2＋y2－2y)＋2xi＝8＋ai，
∴
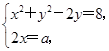消去x，得4(y－1)2＝36－a2.
∵y＞0，∴4(y－1)2≥0，
∴36－a2≥0，－6≤a≤6.
又2x＝a，x＜0，∴a＜0，∴－6≤a＜0.
故a的取值范围是[－6,0)．
又z
＋2i＝8＋ai，故(x2＋y2－2y)＋2xi＝8＋ai，
∴
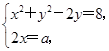消去x，得4(y－1)2＝36－a2.∵y＞0，∴4(y－1)2≥0，
∴36－a2≥0，－6≤a≤6.
又2x＝a，x＜0，∴a＜0，∴－6≤a＜0.
故a的取值范围是[－6,0)．
练习册系列答案
相关题目
是实数，若复数
（
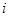为虚数单位）在复平面内对应的点在直线
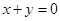上，则
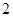
在复平面内对应的点的坐标为 ( )
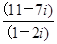(i为虚数单位)，则a＋b＝________．
＝________．
＝________.
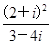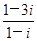+i= .
的虚部为（ ）