题目内容
在锐角△ABC中,角A,B,C所对的边分别为a,b,c.已知 .
.
(Ⅰ)求sinC;
(Ⅱ)当c=2a,且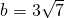 时,求a.
时,求a.
解:(Ⅰ)由已知可得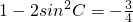 .所以
.所以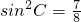 .
.
因为在△ABC中,sinC>0,
所以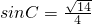 .(6分)
.(6分)
(Ⅱ)因为c=2a,所以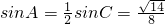 .
.
因为△ABC是锐角三角形,所以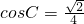 ,
,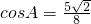 .
.
所以sinB=sin(A+C)=sinAcosC+cosAsinC=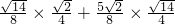 =
=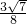 .
.
由正弦定理可得: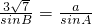 ,所以
,所以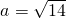 .(13分)
.(13分)
分析:(Ⅰ)利用二倍角公式cos2C=1-2sin2C求解即可,注意隐含条件sinC>0;
(Ⅱ)利用(1)中的结论,结合正弦定理和同角三角函数的关系易得sinA,cosA,cosC的值,又由sinB=sin(A+C)=sinAcosC+cosAsinC求出sinB的值,最后由正弦定理求出a的值.
点评:此类问题是高考的常考题型,主要考查了正弦定理、三角函数及三角恒等变换等知识点,同时考查了学生的基本运算能力和利用三角公式进行恒等变形的技能.
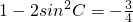 .所以
.所以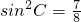 .
.因为在△ABC中,sinC>0,
所以
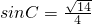 .(6分)
.(6分)(Ⅱ)因为c=2a,所以
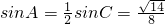 .
.因为△ABC是锐角三角形,所以
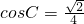 ,
,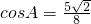 .
.所以sinB=sin(A+C)=sinAcosC+cosAsinC=
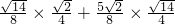 =
=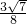 .
.由正弦定理可得:
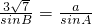 ,所以
,所以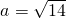 .(13分)
.(13分)分析:(Ⅰ)利用二倍角公式cos2C=1-2sin2C求解即可,注意隐含条件sinC>0;
(Ⅱ)利用(1)中的结论,结合正弦定理和同角三角函数的关系易得sinA,cosA,cosC的值,又由sinB=sin(A+C)=sinAcosC+cosAsinC求出sinB的值,最后由正弦定理求出a的值.
点评:此类问题是高考的常考题型,主要考查了正弦定理、三角函数及三角恒等变换等知识点,同时考查了学生的基本运算能力和利用三角公式进行恒等变形的技能.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目