题目内容
对于指数函数f（x）=ax，“a＞1“是“f（x）在R上的单调”的（ ）
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
根据指数函数f（x）=ax的性质，当a＞1时y=f（x）为R上的单调增函数，
当0＜a＜1时，y=f（x）为R上的单调减函数；
则“a＞1“能得出“f（x）在R上的单调”，
而在R上f（x）在R上的单调，不能推出a＞1，
故“a＞1“是“f（x）在R上的单调”的充分而不必要条件．
故选A．
当0＜a＜1时，y=f（x）为R上的单调减函数；
则“a＞1“能得出“f（x）在R上的单调”，
而在R上f（x）在R上的单调，不能推出a＞1，
故“a＞1“是“f（x）在R上的单调”的充分而不必要条件．
故选A．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
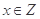,集合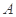
是奇数集,集合
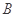是偶数集.若命题
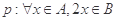,则（ ）
