题目内容
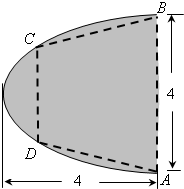 如图,有一块抛物线形状的钢板,计划将此钢板切割成等腰梯形ABCD的形状,使得A,B,C,D都落在抛物线上,点A,B关于抛物线的对称轴对称且AB=4,抛物线的顶点到底边AB的距离是4,记CD=2t,梯形面积为S.以抛物线的顶点为坐标原点,其对称轴为x轴,建立平面直角坐标系.
如图,有一块抛物线形状的钢板,计划将此钢板切割成等腰梯形ABCD的形状,使得A,B,C,D都落在抛物线上,点A,B关于抛物线的对称轴对称且AB=4,抛物线的顶点到底边AB的距离是4,记CD=2t,梯形面积为S.以抛物线的顶点为坐标原点,其对称轴为x轴,建立平面直角坐标系.(1)求出钢板轮廓所在抛物线的方程;
(2)求面积S关于t的函数解析式,并写出其定义域;
(3)求面积S的最大值.
分析:(1)以题意建立坐标系,设出抛物线方程,把B点坐标代入抛物线方程求解p,则抛物线的方程可求;
(2)由CD=t,利用t表示出C点的坐标,则等腰梯形ABCD的上底及高可用含有t的代数式表示,然后直接写出梯形的面积公式,由梯形的上底长大于0小于4,且梯形的高大于0解得t的范围;
(3)求出(2)中函数的导函数,得到极大值,也就是梯形面积的最大值.
(2)由CD=t,利用t表示出C点的坐标,则等腰梯形ABCD的上底及高可用含有t的代数式表示,然后直接写出梯形的面积公式,由梯形的上底长大于0小于4,且梯形的高大于0解得t的范围;
(3)求出(2)中函数的导函数,得到极大值,也就是梯形面积的最大值.
解答: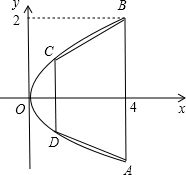 解:如图,
解:如图,
(1)设钢板轮廓所在抛物线的方程为:y2=2px(p>0),
由图得抛物线过点(4,2),代入y2=2px(p>0),得p=
,
所钢板轮廓所在抛物线的方程为y2=x.
(2)由CD=2t,故可设C(t2,t),梯形高为4-t2,
梯形的面积S=
(2t+4)(4-t2)=-t3-2t2+4t+8,
又由
,得0<t<2,故其定义域为(0,2).
(3)由(2)知S=-t3-2t2+4t+8(0<t<2),S'=-3t2-4t+4,
令S'=0,得t=
,
列表如下:
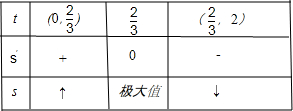
由上表知面积S在t=
时取到极大值,又S在(0,2)只有一个极值点,
故极大值也为最大值,此时Smax=
.
 解:如图,
解:如图,(1)设钢板轮廓所在抛物线的方程为:y2=2px(p>0),
由图得抛物线过点(4,2),代入y2=2px(p>0),得p=
| 1 |
| 2 |
所钢板轮廓所在抛物线的方程为y2=x.
(2)由CD=2t,故可设C(t2,t),梯形高为4-t2,
梯形的面积S=
| 1 |
| 2 |
又由
|
(3)由(2)知S=-t3-2t2+4t+8(0<t<2),S'=-3t2-4t+4,
令S'=0,得t=
| 2 |
| 3 |
列表如下:

由上表知面积S在t=
| 2 |
| 3 |
故极大值也为最大值,此时Smax=
| 256 |
| 27 |
点评:本题考查了函数解析式的求解的方法,注意的是实际问题要有实际意义,考查了利用导数研究函数的极值,注意极值与最值得关系,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
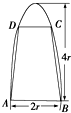 如图,有一块抛物线形钢板,其垂直于对称轴的边界线AB长为2r,高为4r,计划将此钢板切割成等腰梯形的形状,以AB为下底,上底CD的端点在抛物线上,记CD=2x,梯形面积为S.求面积S,使其为以x为自变量的函数式,并写出其定义域.
如图,有一块抛物线形钢板,其垂直于对称轴的边界线AB长为2r,高为4r,计划将此钢板切割成等腰梯形的形状,以AB为下底,上底CD的端点在抛物线上,记CD=2x,梯形面积为S.求面积S,使其为以x为自变量的函数式,并写出其定义域.