题目内容
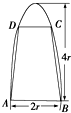 如图,有一块抛物线形钢板,其垂直于对称轴的边界线AB长为2r,高为4r,计划将此钢板切割成等腰梯形的形状,以AB为下底,上底CD的端点在抛物线上,记CD=2x,梯形面积为S.求面积S,使其为以x为自变量的函数式,并写出其定义域.
如图,有一块抛物线形钢板,其垂直于对称轴的边界线AB长为2r,高为4r,计划将此钢板切割成等腰梯形的形状,以AB为下底,上底CD的端点在抛物线上,记CD=2x,梯形面积为S.求面积S,使其为以x为自变量的函数式,并写出其定义域.分析:建立平面直角坐标系,则B(r,-4r),设抛物线方程为x2=-2py(p>0),代入确定抛物线的方程,进而确定点C的纵坐标,由此可得梯形的面积及函数的定义域.
解答: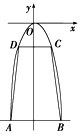 解:建立如图所示的平面直角坐标系xOy,则B(r,-4r)
解:建立如图所示的平面直角坐标系xOy,则B(r,-4r)
设抛物线方程为x2=-2py(p>0)
∵B(r,-4r)在抛物线上,
∴r2=8pr,
∴p=
∴抛物线方程为x2=-
y
∵C的横坐标为x,则点C的纵坐标为y=-
∴梯形ABCD的高为h=4r-
∴S=
(2r+2x)•(4r-
)=
(x+r)(r2-x2)
其定义域为(0,r).
 解:建立如图所示的平面直角坐标系xOy,则B(r,-4r)
解:建立如图所示的平面直角坐标系xOy,则B(r,-4r)设抛物线方程为x2=-2py(p>0)
∵B(r,-4r)在抛物线上,
∴r2=8pr,
∴p=
| r |
| 8 |
∴抛物线方程为x2=-
| r |
| 4 |
∵C的横坐标为x,则点C的纵坐标为y=-
| 4x2 |
| r |
∴梯形ABCD的高为h=4r-
| 4x2 |
| r |
∴S=
| 1 |
| 2 |
| 4x2 |
| r |
| 4 |
| r |
其定义域为(0,r).
点评:本题考查抛物线的运用,考查梯形面积的计算,确定抛物线的解析式是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目