题目内容
已知A(2,0),P(sin(2t-60°),cos(2t-60°)),当t由20°变到40°时,P点从P1按顺时针运动至P2的曲线轨迹与线段AP1,AP2所围成的图形面积是
.
| π |
| 9 |
| π |
| 9 |
分析:如图所示,把问题转化为S弓形P1P2+S△AP1P2,等价于求S扇形OP1P2即可.
解答:解:如图所示,点 P位于单位圆x2+y2=1上.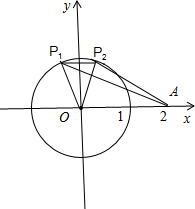
当t=20°时,2t-60°=-20°,点P(sin(-20°),cos20°),即P(cos110°,sin110°).
当t=40°时,2t-60°=20°,点P(sin20°,cos20°),即P(cos70°,sin70°).
连接P1P2,则P1P2∥x轴.
∴S△AP1P2=S△OP1P2.
因此P点从P1按顺时针运动至P2的曲线轨迹与线段AP1,AP2所围成的图形面积
=S弓形P1P2+S△AP1P2=S扇形OP1P2=
×
×12=
.
故答案为
.

当t=20°时,2t-60°=-20°,点P(sin(-20°),cos20°),即P(cos110°,sin110°).
当t=40°时,2t-60°=20°,点P(sin20°,cos20°),即P(cos70°,sin70°).
连接P1P2,则P1P2∥x轴.
∴S△AP1P2=S△OP1P2.
因此P点从P1按顺时针运动至P2的曲线轨迹与线段AP1,AP2所围成的图形面积
=S弓形P1P2+S△AP1P2=S扇形OP1P2=
| 1 |
| 2 |
| 2π |
| 9 |
| π |
| 9 |
故答案为
| π |
| 9 |
点评:把问题转化为S弓形P1P2+S△AP1P2,等价于求S扇形OP1P2及熟练掌握“等积变形”和扇形的面积计算公式是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目