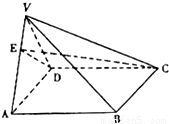
题目内容
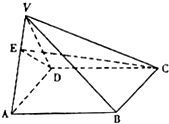
如图，四棱锥V-ABCD中，底面ABCD是边长为2的正方形，其它侧面都是侧棱长为| 5 |
分析：因为侧面VAB为等腰三角形，故取AB的中的E有VE⊥AB，因为底面ABCD是边长为2的正方形，取CD的中点F，则EF⊥AB，所以∠VEF为二面角V-AB-C的平面角，再解△VEF即可．
解答：解：取AB、CD的中点E、F，连接VE、EF、VF
∵VA=VB=
∴△VAB为等腰三角形
∴VE⊥AB
又∵ABCD是正方形，则BC⊥AB
∵EF∥BC
∴EF⊥AB
∵EF∩VE=E
∴∠VEF为二面角V-AB-C的平面角
∵△VAB≌△VDC∴VE=VF=2
EF=BC=2
∴△VEF为等边三角形
∴∠VEF=60°
即二面角V-AB-C为60°
∵VA=VB=
| 5 |
∴△VAB为等腰三角形
∴VE⊥AB
又∵ABCD是正方形，则BC⊥AB
∵EF∥BC
∴EF⊥AB
∵EF∩VE=E
∴∠VEF为二面角V-AB-C的平面角
∵△VAB≌△VDC∴VE=VF=2
EF=BC=2
∴△VEF为等边三角形
∴∠VEF=60°
即二面角V-AB-C为60°
点评：本题考查二面角的求法和对正棱锥的认识，考查识图能力和运算能力．
练习册系列答案
相关题目
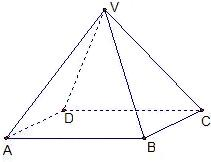
（2012•许昌县一模）如图，四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD三角形，平面VAD⊥底面ABCD，设AB=2
（2012•许昌县一模）如图，四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ASCD．设AB=2．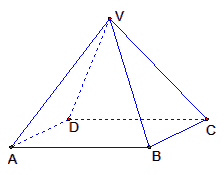
如图，四棱锥V-ABCD中，底面ABCD是边长为2的正方形，其它侧面都是侧棱长为
的等腰三角形，求二面角V-AB-C的大小. 