题目内容
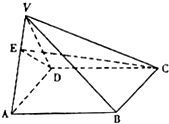 (2012•许昌县一模)如图,四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD三角形,平面VAD⊥底面ABCD,设AB=2
(2012•许昌县一模)如图,四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD三角形,平面VAD⊥底面ABCD,设AB=2(I)证明:AB⊥平面VAD;
(II)求二面角A-VD-B的正切值;
(III) E是VA上的动点,当面DCE⊥面VAB时,求三棱锥V-ECD的体积.
分析:(I)欲证AB⊥面VAD,根据直线与平面垂直的判定定理可知只需证AB与面VAD内两相交直线垂直,而VE⊥AB可由面VAD⊥底面ABCD得到,AB⊥CD,满足定理条件;
(II)设VD的中点为F,连AF,AF⊥VD,由三垂线定理知BF⊥VD,根据二面角平面角的定义可知∠AFB是面VAD与面VDB所成的二面角的平面角,在Rt△ABF中求出此角即可.
(III)由(Ⅰ)可知AB⊥平面VAD,说明平面VAD⊥平面ECD.当E是VA的中点时,证明面DCE⊥面VAB,利用三棱锥V-ECD的体积等于三棱锥C-EVD的体积,求解即可
(II)设VD的中点为F,连AF,AF⊥VD,由三垂线定理知BF⊥VD,根据二面角平面角的定义可知∠AFB是面VAD与面VDB所成的二面角的平面角,在Rt△ABF中求出此角即可.
(III)由(Ⅰ)可知AB⊥平面VAD,说明平面VAD⊥平面ECD.当E是VA的中点时,证明面DCE⊥面VAB,利用三棱锥V-ECD的体积等于三棱锥C-EVD的体积,求解即可
解答: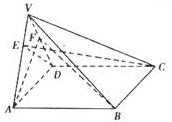 证明:(I)由于面VAD是正三角形,设AD的中点为E,
证明:(I)由于面VAD是正三角形,设AD的中点为E,
则VE⊥AD,而面VAD⊥底面ABCD,则VE⊥AB.
又面ABCD是正方形,则AB⊥CD,故AB⊥面VAD.
(II)由AB⊥面VAD,则点B在平面VAD内的射影是A,
设VD的中点为F,连AF,BF由△VAD是正△,则AF⊥VD,
由三垂线定理知BF⊥VD,
故∠AFB是面VAD与面VDB所成的二面角的平面角.
设正方形ABCD的边长为a,
则在Rt△ABF中,,AB=a,AF=
a,tan∠AFB=
=
=
故二面角A-VD-B的正切值为:
;
(III):由(Ⅰ)可知AB⊥平面VAD,
∴CD⊥平面VAD.
∴平面VAD⊥平面ECD.
又∵△VAD是正三角形,
∴当E是VA的中点时,ED⊥VA.
∴VA⊥平面EDC.
∴面DCE⊥面VAB
三棱锥V-ECD的体积等于三棱锥C-EVD的体积,
VC-VED=
•S△VED•DC=
×
×
×1×2=
.12分
 证明:(I)由于面VAD是正三角形,设AD的中点为E,
证明:(I)由于面VAD是正三角形,设AD的中点为E,则VE⊥AD,而面VAD⊥底面ABCD,则VE⊥AB.
又面ABCD是正方形,则AB⊥CD,故AB⊥面VAD.
(II)由AB⊥面VAD,则点B在平面VAD内的射影是A,
设VD的中点为F,连AF,BF由△VAD是正△,则AF⊥VD,
由三垂线定理知BF⊥VD,
故∠AFB是面VAD与面VDB所成的二面角的平面角.
设正方形ABCD的边长为a,
则在Rt△ABF中,,AB=a,AF=
| ||
| 2 |
| AB |
| AF |
| a | ||||
|
2
| ||
| 3 |
故二面角A-VD-B的正切值为:
2
| ||
| 3 |
(III):由(Ⅰ)可知AB⊥平面VAD,
∴CD⊥平面VAD.
∴平面VAD⊥平面ECD.
又∵△VAD是正三角形,
∴当E是VA的中点时,ED⊥VA.
∴VA⊥平面EDC.
∴面DCE⊥面VAB
三棱锥V-ECD的体积等于三棱锥C-EVD的体积,
VC-VED=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
点评:本题主要考查了直线与平面垂直的判定,几何体的体积的求法,以及二面角及其度量,对于二面角的度量在高考中有所弱化,属于综合题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•许昌县一模)某学校对高一新生的体重进行了抽样调查.右图是根据抽样调查后的数据绘制的频率分布直方图,其中体重(单位:kg)的范围是[45,70],样本数据分组为[45,50),[50,55),[55,60),[60,65),[65,70],已知被调查的学生中体重不足55kg的有36,则被调查的高一新生体重在50kg至65kg的人数是.( )
(2012•许昌县一模)某学校对高一新生的体重进行了抽样调查.右图是根据抽样调查后的数据绘制的频率分布直方图,其中体重(单位:kg)的范围是[45,70],样本数据分组为[45,50),[50,55),[55,60),[60,65),[65,70],已知被调查的学生中体重不足55kg的有36,则被调查的高一新生体重在50kg至65kg的人数是.( ) (2012•许昌县一模)一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )
(2012•许昌县一模)一个几何体按比例绘制的三视图如图所示(单位:m),则该几何体的体积为( )