题目内容
已知过原点的直线与圆（x+2）2+y2=1相切，若切点在第二象限，则该直线的方程为
x+y=0
x+y=0．
| ||
| 3 |
| ||
| 3 |
分析：可设切线方程为kx-y=0，然后根据直线与圆相切的性质可知，圆心到直线kx-y=0的距离d=1，可求k，然后切点在第二象限，即切线经过第二象限即可求解
解答：解：设切线方程为y=kx即kx-y=0
根据直线与圆相切的性质可知，圆心（-2，0）到直线kx-y=0的距离d=
=1
解可得，k=±
∴切点在第二象限，即切线经过第二象限
∴k＜0
∴k=-
则切线方程为
x+y=0
故答案为：
x+y=0
根据直线与圆相切的性质可知，圆心（-2，0）到直线kx-y=0的距离d=
| |-2k| | ||
|
解可得，k=±
| ||
| 3 |
∴切点在第二象限，即切线经过第二象限
∴k＜0
∴k=-
| ||
| 3 |
则切线方程为
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题主要考查了直线与圆相切性质的应用，解题的关键是点到直线距离公式的应用．
练习册系列答案
相关题目
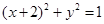相切，若切点在第二象限，则该直线的方程为 ．