题目内容
已知过原点的直线与圆 相切,若切点在第二象限,则该直线的方程为 .
相切,若切点在第二象限,则该直线的方程为 .
【答案】
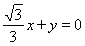
【解析】
试题分析:设切线方程为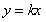 即
即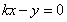 ,根据直线与圆相切的性质可知,圆心
,根据直线与圆相切的性质可知,圆心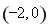 到直线
到直线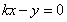 的距离
的距离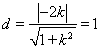 ,解可得,
,解可得,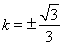 ,因为切点在第二象限,即切线经过第二象限,∴
,因为切点在第二象限,即切线经过第二象限,∴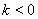 ,∴
,∴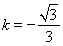 ,则切线方程为
,则切线方程为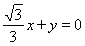 故答案为:
故答案为: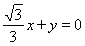 .
.
考点:直线与圆的位置关系.

练习册系列答案
相关题目
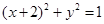 相切,若切点在第二象限,则该直线的方程为 .
相切,若切点在第二象限,则该直线的方程为 .