题目内容
求使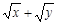 ≤
≤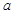
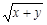 (x>0,y>0)恒成立的
(x>0,y>0)恒成立的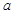 的最小值
的最小值
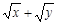 ≤
≤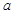
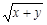 (x>0,y>0)恒成立的
(x>0,y>0)恒成立的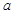 的最小值
的最小值 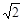
本题主要考查了基本不等式的综合.(1)解决恒成立问题一定要搞清谁是自变量,谁是参数.一般地,知道谁的范围,谁就是变量,求谁的范围,谁就是参数;(2)对于二次不等式恒成立问题,恒大于0就是相应的二次函数的图象在给定的区间上全部在x轴上方,
恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴下方.先将题设的不等式平方后,同时利用基本不等式综合可求得a的最小值满足的等式求得a.
解法一 由于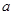 的值为正数,将已知不等式两边平方,得
的值为正数,将已知不等式两边平方,得
x+y+2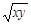 ≤
≤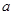 2(x+y),即2
2(x+y),即2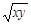 ≤(
≤(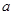 2-1)(x+y), ①
2-1)(x+y), ①
∴x,y>0,∴x+y≥2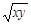 , ②
, ②
当且仅当x=y时,②中有等号成立
比较①、②得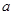 的最小值满足
的最小值满足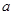 2-1=1,
2-1=1,
∴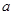 2=2,
2=2,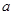 =
=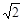 (因
(因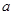 >0),∴
>0),∴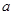 的最小值是
的最小值是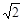
解法二 设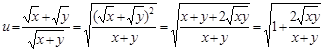
∵x>0,y>0,∴x+y≥2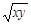 (当x=y时“=”成立),
(当x=y时“=”成立),
恒小于0就是相应的二次函数的图象在给定的区间上全部在x轴下方.先将题设的不等式平方后,同时利用基本不等式综合可求得a的最小值满足的等式求得a.
解法一 由于
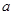 的值为正数,将已知不等式两边平方,得
的值为正数,将已知不等式两边平方,得 x+y+2
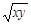 ≤
≤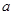 2(x+y),即2
2(x+y),即2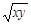 ≤(
≤(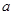 2-1)(x+y), ①
2-1)(x+y), ①∴x,y>0,∴x+y≥2
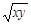 , ②
, ②当且仅当x=y时,②中有等号成立
比较①、②得
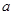 的最小值满足
的最小值满足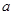 2-1=1,
2-1=1,∴
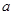 2=2,
2=2,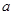 =
=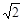 (因
(因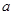 >0),∴
>0),∴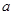 的最小值是
的最小值是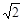
解法二 设
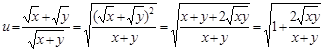
∵x>0,y>0,∴x+y≥2
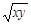 (当x=y时“=”成立),
(当x=y时“=”成立),
练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
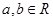 ,求证:
,求证: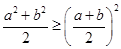
 ,
, ,求证:
,求证: ;
; ,且
,且 , 求证:
, 求证: 与
与 中至少有一个小于2.
中至少有一个小于2.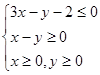 ,若目标函数z=ax+by(a>0,b>0)的最大值为1,则
,若目标函数z=ax+by(a>0,b>0)的最大值为1,则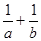 的最小值为 ( )
的最小值为 ( ) 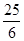

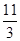
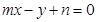 过点(2,1),其中
过点(2,1),其中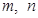 是正数,则
是正数,则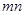 的最大值为
的最大值为
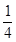
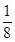

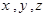 满足
满足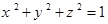 则
则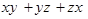 的取值范围是 ( )
的取值范围是 ( )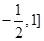


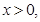 则
则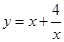 的最小值是 ( )
的最小值是 ( )



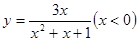 的值域是( )
的值域是( )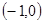
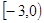
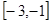
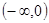
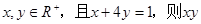 的最大值为
的最大值为