题目内容
15. 已知抛物线y2=2px(p>0)焦点为F,抛物线上横坐标为$\frac{1}{2}$的点到抛物线顶点的距离与其到准线的距离相等.
已知抛物线y2=2px(p>0)焦点为F,抛物线上横坐标为$\frac{1}{2}$的点到抛物线顶点的距离与其到准线的距离相等.(Ⅰ)求抛物线的方程;
(Ⅱ)设过点P(6,0)的直线l与抛物线交于A,B两点,若以AB为直径的圆过点F,求直线l的方程.
分析 (Ⅰ)确定抛物线上横坐标为$\frac{1}{2}$的点的坐标为($\frac{1}{2}$,$±\sqrt{p}$),利用抛物线上横坐标为$\frac{1}{2}$的点到抛物线顶点的距离与其到准线的距离相等,求出p,即可求抛物线的方程;
(Ⅱ)设直线l:x=my+6,代入y2=4x得,y2-4my-24=0,利用以AB为直径的圆过点F,可得FA⊥FB,即$\overrightarrow{FA}•\overrightarrow{FB}$=0,可得:(x1-1)(x2-1)+y1y2=0,即可求直线l的方程.
解答 解:(Ⅰ)抛物线上横坐标为$\frac{1}{2}$的点的坐标为($\frac{1}{2}$,$±\sqrt{p}$),到抛物线顶点的距离的平方为$\frac{1}{4}+p$,
∵抛物线上横坐标为$\frac{1}{2}$的点到抛物线顶点的距离与其到准线的距离相等,
∴$\frac{1}{4}+p$=($\frac{1}{2}$+$\frac{p}{2}$)2,
∴p=2
抛物线的方程为:y2=4x.…(6分)
(Ⅱ)由题意可知,直线l不垂直于y轴
可设直线l:x=my+6,代入y2=4x得,y2-4my-24=0,
设A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=-24,
∵以AB为直径的圆过点F,∴FA⊥FB,即$\overrightarrow{FA}•\overrightarrow{FB}$=0
可得:(x1-1)(x2-1)+y1y2=0
∴(1+m2)y1y2+5m(y1+y2)+25=0
∴-24(1+m2)+20m2+25=0,
解得:m=±$\frac{1}{2}$,
∴直线l:x=±$\frac{1}{2}$y+6,即l:2x±y-12=0.…(15分)
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

| A. | 有最小值-1,最大值$\frac{7}{3}$ | B. | 有最小值2,无最大值 | ||
| C. | 有最大值$\frac{7}{3}$,无最小值 | D. | 有最小值-1,无最大值 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
p1:函数y=ax+x(a>0,且a≠1)在R上为增函数;
p2:?a,b∈R,a2-ab+b2<0;
p3:cosα=cosβ成立的一个充分不必要条件是α=2kπ+β(k∈Z).
则下列命题中的真命题为( )
| A. | p1∨p2 | B. | p2∧p3 | C. | p1∨¬p3 | D. | ¬p2∧p3 |
| A. | [e-1,2] | B. | [e-2,2] | C. | [$\frac{1}{e}$-e,1+e] | D. | [1-e,1+e] |
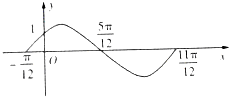 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象过点(0,1)
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象过点(0,1)