题目内容
10.已知侧棱垂直于底面且底面为正三角形的棱柱的体积为16,则其表面积取最小值时,底面边长为4.分析 由题意设出直三棱柱的底面边长和高,由体积列式得到底面边长和高的关系,写出表面积,利用导数求最值并得到表面积最小时的底面边长.
解答 解:由题意可知,三棱柱为直三棱柱,
设其底面边长为a,高为h(a>0,h>0),
则$V=\frac{1}{2}a•\frac{\sqrt{3}}{2}a•h=16$,∴$h=\frac{64}{\sqrt{3}{a}^{2}}$,
则$S=3ah+\frac{\sqrt{3}}{2}{a}^{2}$=$\frac{192}{\sqrt{3}a}+\frac{\sqrt{3}}{2}{a}^{2}$,
${S}^{′}=-\frac{192}{\sqrt{3}{a}^{2}}+\sqrt{3}a$,
由S′=0,得a=4.
∴当a∈(0,4)时,S′<0,当a∈(4,+∞)时,S′>0,
∴当a=4时S有最小值.
故答案为:4.
点评 本题考查了空间几何体的表面积和体积,考查了利用导数求函数的最值,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.如图所示,用符号语言可表示为( )
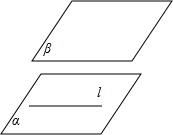

| A. | α∩β=l | B. | α∥β,l∈α | C. | l∥β,l?α | D. | α∥β,l?α |
 正三棱台的上、下底面的边长分别是3和6.
正三棱台的上、下底面的边长分别是3和6.