题目内容
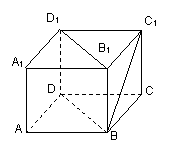
如图,设平面AC与平面BD相交于BC,它们所成的一个二面角为45°,P∈平面AC,Q∈平面BD,已知直线MQ是直线PQ在平面BD内的射影,且M在BC上,又直线PQ与平面BD所成的角为β,∠CMQ=![]() ,(0°<
,(0°<![]() <90°),设线段PM=a,求PQ的长.
<90°),设线段PM=a,求PQ的长.

答案:
解析:
提示:
解析:
|
解:设PMR=α,作PR⊥MQ于R,显然PR⊥平面BD. 作RN⊥BC于N,连PN,则PN⊥BC.∴∠PNR=45°,∠PQM=β. 在直角ΔPMR中:PR=asinα,MR=acosα. 在直角ΔMNR中:NR=MRsin ∵PR=NR,∴asinα=acosαsin ∴tanα=sin 在ΔPMQ中由正弦定理: ∴PQ= 评析:本题是利用正弦定理通过解斜三角形求出PQ的长,当然也可以通过三个直角三角形中的关系转换,先出求PR,最后在直角ΔPQR中利用锐角函数处理,相比之下,还是给出的解法略为简便些. |
提示:
|
在ΔPMQ中因为PM=a,∠PQM=β,欲求PQ的长,根据正弦定理只要能求出sin∠PMR就行了. |

练习册系列答案
相关题目
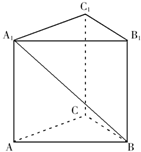 棱长均为a的正三棱柱ABC-A1B1C1(如图),求A1B与平面BB1C1C所成角的大小.
棱长均为a的正三棱柱ABC-A1B1C1(如图),求A1B与平面BB1C1C所成角的大小.
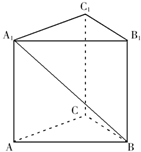 棱长均为a的正三棱柱ABC-A1B1C1(如图),求A1B与平面BB1C1C所成角的大小.
棱长均为a的正三棱柱ABC-A1B1C1(如图),求A1B与平面BB1C1C所成角的大小.