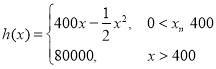题目内容
【题目】已知命题p:![]() ,q:
,q: ![]() ≤0.
≤0.
(1)若p是q的充分而不必要条件,求实数m的取值范围;
(2)若q是p的必要而不充分条件,求实数m的取值范围.
【答案】(1) (-∞,-8)∪(21,+∞). (2) [-3,16].
【解析】
分别解出![]() 的解集,再根据“p是q的充分而不必要条件”与“q是p的必要而不充分条件”列出解集的区间端点满足的不等式再求解即可.
的解集,再根据“p是q的充分而不必要条件”与“q是p的必要而不充分条件”列出解集的区间端点满足的不等式再求解即可.
解:(1)由![]() |解得-2≤x≤10,所以命题p:-2≤x≤10.设满足条件p的元素构成的集合为A,则A={x|-2≤x≤10}
|解得-2≤x≤10,所以命题p:-2≤x≤10.设满足条件p的元素构成的集合为A,则A={x|-2≤x≤10}
由![]() ≤0,得
≤0,得![]() ≤x≤
≤x≤![]() ,所以命题q:
,所以命题q:![]() ≤x≤
≤x≤![]() .
.
设满足条件q的元素构成的集合为B,
则B=![]() .
.
命题q:x<![]() 或x>
或x>![]() .
.
设满足条件q的元素构成的集合为C,
则C=![]() .
.
因为p是q的充分而不必要条件,所以AC,
所以![]() >10或
>10或![]() <-2,解得m>21或m<-8.
<-2,解得m>21或m<-8.
所以实数m的取值范围为(-∞,-8)∪(21,+∞).
(2)解:(法一)命题p:x<-2或x>10.
设满足条件p的元素构成的集合为D,
则D={x|x<-2或x>10}.
因为q是p的必要而不充分条件,所以DC,
所以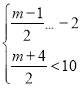 或
或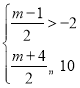
解得-3≤m≤16.
所以实数m的取值范围为[-3,16].
(法二)因为q是p的必要而不充分条件,
所以p是q的必要而不充分条件,所以BA,
所以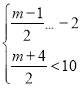 或
或
解得-3≤m≤16.
所以实数m的取值范围为[-3,16].

【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,部分统计数据如下表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅰ)根据以上![]() 列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
(Ⅱ)从学习成绩优秀的12名同学中,随机抽取2名同学,求抽到不使用智能手机的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.05 | 0,。025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |