题目内容
若离散型随机变量ξ的分布列为
则常数c的值为
．
| ξ | 0 | 1 |
| P | 9c2-c | 3-8c |
| 1 |
| 3 |
| 1 |
| 3 |
分析：根据离散型随机变量ξ的分布列的定义和性质可得 9c2-c+（3-8c）=1，且9c2-c＞0，（3-8c）＞0，由此求得常数c的值．
解答：解：根据离散型随机变量ξ的分布列的定义和性质可得 9c2-c+（3-8c）=1，且9c2-c＞0，（3-8c）＞0．
解得c=
，
故答案为
．
解得c=
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评：本题主要考查离散型随机变量的分布列的定义和性质应用，属于中档题．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
若离散型随机变量X的分布表如右图所示，则常数c= ．
| X | 0 | 1 |
| P | 9c2-c | 3-8c |
以下四个命题：
①由圆的过圆心的弦最长的性质类比出球的过球心的截面面积最大的性质；
②若（3x-1）7=a7x7+a6x6+…+a1x+a0，则a7+a6+…+a1=129；
③在含有5件次品的100件产品中，任取3件，则取到两件次品的概率为
；
④若离散型随机变量X的方差为D（X）=2，则D（2X-1）=8．
其中正确命题的序号是（ ）
①由圆的过圆心的弦最长的性质类比出球的过球心的截面面积最大的性质；
②若（3x-1）7=a7x7+a6x6+…+a1x+a0，则a7+a6+…+a1=129；
③在含有5件次品的100件产品中，任取3件，则取到两件次品的概率为
| ||||
|
④若离散型随机变量X的方差为D（X）=2，则D（2X-1）=8．
其中正确命题的序号是（ ）
| A、①②④ | B、①②③④ |
| C、①② | D、①③④ |
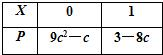若离散型随机变量X的分布列如图，则常数c的值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
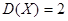，则
；
；
，则
．
；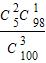