题目内容
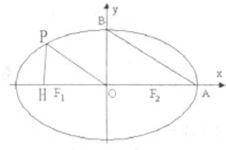 如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
(1)求证:当a取定值时,点H必为定点;
(2)如果点H落在左顶点与左焦点之间,试求椭圆离心率的取值范围;
(3)如果以OP为直径的圆与直线AB相切,且凸四边形ABPH的面积等于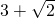 ,求椭圆的方程.
,求椭圆的方程.
 解:(1)由
解:(1)由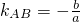 ,OP∥AB,得
,OP∥AB,得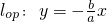 ,
,代入椭圆方程
 ,得
,得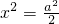 ,
,∴
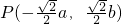 或
或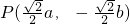 ,
,∵PH⊥x轴,∴
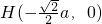 或
或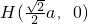 ,
,∵a为定值,∴H为定点;(4分)
(2)∵点H落在左顶点与左焦点之间,
∴只有
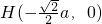 ,且
,且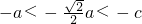 ,
,可解得
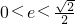 ;(4分)
;(4分)(3)以OP为直径的圆与直线AB相切等价于点O到直线AB的距离等于
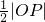 .
.由条件设直线
 ,
,则点O到直线AB的距离
 ,又
,又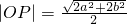 ,
,∴
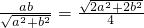 得
得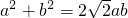 ①
①又由
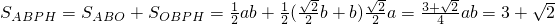 ,
,得ab=4.②由①②解得
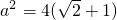 ,
, ,
,所以所求椭圆方程为:
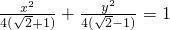 .(6分)
.(6分)分析:(1)由
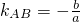 ,OP∥AB,得
,OP∥AB,得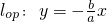 ,代入椭圆方程
,代入椭圆方程 ,得
,得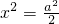 ,由此能够证明当a取定值时,点H必为定点.
,由此能够证明当a取定值时,点H必为定点.(2)由点H落在左顶点与左焦点之间,知只有
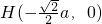 ,且
,且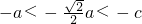 ,由此能求出椭圆离心率的取值范围.
,由此能求出椭圆离心率的取值范围.(3)以OP为直径的圆与直线AB相切等价于点O到直线AB的距离等于
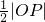 .由条件设直线
.由条件设直线 ,点O到直线AB的距离
,点O到直线AB的距离 ,又
,又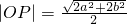 ,所以
,所以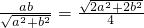 ,再由
,再由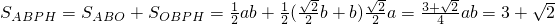 ,
,能够得到所求椭圆方程.
点评:本题考查定点的证明、离心率取值范围的确定和椭圆方程的求法,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
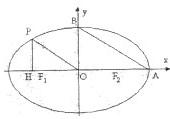
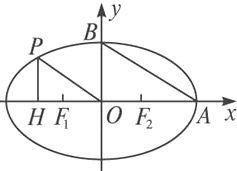 如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.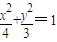 中,F1,F2分别为椭圆C的左右两个焦点,P为椭圆上且在第一象限内的点,△PF1F2的重心为G,内心为I.
中,F1,F2分别为椭圆C的左右两个焦点,P为椭圆上且在第一象限内的点,△PF1F2的重心为G,内心为I.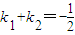 ,求直线l的方程.
,求直线l的方程.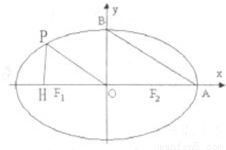 如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.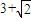 ,求椭圆的方程.
,求椭圆的方程.