题目内容
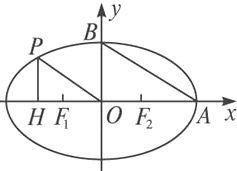 如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.(1)求证:当a取定值时,点H必为定点;
(2)如果点H落在左顶点与左焦点之间,试求椭圆离心率的取值范围;
(3)如果以OP为直径的圆与直线AB相切,且凸四边形ABPH的面积等于3+
| 2 |
分析:(1)由kAB=-
,OP∥AB,得lop:y=-
x,代入椭圆方程
+
=1,得x2=
,由此能够证明当a取定值时,点H必为定点.
(2)由点H落在左顶点与左焦点之间,知只有H(-
a,0),且-a<-
a<-c,由此能求出椭圆离心率的取值范围.
(3)以OP为直径的圆与直线AB相切等价于点O到直线AB的距离等于
|OP|.由条件设直线AB:
+
=1,点O到直线AB的距离d=
,又|OP|=
,所以
=
,再由SABPH=SABO+SOBPH=
ab+
(
b+b)
a=
ab=3+
,
能够得到所求椭圆方程.
| b |
| a |
| b |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 2 |
(2)由点H落在左顶点与左焦点之间,知只有H(-
| ||
| 2 |
| ||
| 2 |
(3)以OP为直径的圆与直线AB相切等价于点O到直线AB的距离等于
| 1 |
| 2 |
| x |
| a |
| y |
| b |
| ab | ||
|
| ||
| 2 |
| ab | ||
|
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
3+
| ||
| 4 |
| 2 |
能够得到所求椭圆方程.
解答: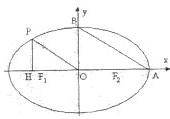 解:(1)由kAB=-
解:(1)由kAB=-
,OP∥AB,得lop:y=-
x,
代入椭圆方程
+
=1,得x2=
,
∴P(-
a,
b)或P(
a,-
b),
∵PH⊥x轴,∴H(-
a,0)或H(
a,0),
∵a为定值,∴H为定点;(4分)
(2)∵点H落在左顶点与左焦点之间,
∴只有H(-
a,0),且-a<-
a<-c,
可解得0<e<
;(4分)
(3)以OP为直径的圆与直线AB相切等价于点O到直线AB的距离等于
|OP|.
由条件设直线AB:
+
=1,
则点O到直线AB的距离d=
,又|OP|=
,
∴
=
得a2+b2=2
ab①
又由SABPH=SABO+SOBPH=
ab+
(
b+b)
a=
ab=3+
,
得ab=4.②由①②解得a2=4(
+1),b2=4(
-1),
所以所求椭圆方程为:
+
=1.(6分)
 解:(1)由kAB=-
解:(1)由kAB=-| b |
| a |
| b |
| a |
代入椭圆方程
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 2 |
∴P(-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∵PH⊥x轴,∴H(-
| ||
| 2 |
| ||
| 2 |
∵a为定值,∴H为定点;(4分)
(2)∵点H落在左顶点与左焦点之间,
∴只有H(-
| ||
| 2 |
| ||
| 2 |
可解得0<e<
| ||
| 2 |
(3)以OP为直径的圆与直线AB相切等价于点O到直线AB的距离等于
| 1 |
| 2 |
由条件设直线AB:
| x |
| a |
| y |
| b |
则点O到直线AB的距离d=
| ab | ||
|
| ||
| 2 |
∴
| ab | ||
|
| ||
| 4 |
| 2 |
又由SABPH=SABO+SOBPH=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
3+
| ||
| 4 |
| 2 |
得ab=4.②由①②解得a2=4(
| 2 |
| 2 |
所以所求椭圆方程为:
| x2 | ||
4(
|
| y2 | ||
4(
|
点评:本题考查定点的证明、离心率取值范围的确定和椭圆方程的求法,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
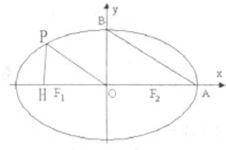 如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.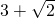 ,求椭圆的方程.
,求椭圆的方程.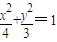 中,F1,F2分别为椭圆C的左右两个焦点,P为椭圆上且在第一象限内的点,△PF1F2的重心为G,内心为I.
中,F1,F2分别为椭圆C的左右两个焦点,P为椭圆上且在第一象限内的点,△PF1F2的重心为G,内心为I.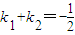 ,求直线l的方程.
,求直线l的方程.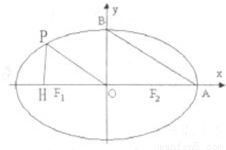 如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.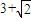 ,求椭圆的方程.
,求椭圆的方程.