题目内容
等差数列 的前
的前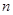 项和为
项和为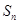 ,且
,且 ,则公差
,则公差 等于( )
等于( )
A. | B. | C.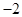 | D. |
C
解析试题分析:∵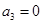 ,即
,即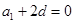 ,∴
,∴ ,∴
,∴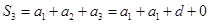 =
= ,∴
,∴ .
.
考点:等差数列的通项公式与前n项和公式.

练习册系列答案
相关题目
等差数列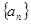 中,若
中,若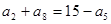 ,则
,则 等于( )
等于( )
| A.3 | B.4 | C.5 | D.6 |
等差数列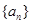 中,已知
中,已知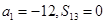 ,使得
,使得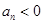 的最大正整数
的最大正整数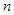 为( )
为( )
A.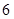 | B. | C. | D. |
等差数列前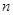 项和为
项和为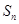 ,若
,若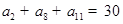 ,则
,则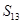 的值是( )
的值是( )
| A. 130 | B. 65 | C. 70 | D. 75 |
已知
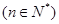 .我们把使乘积
.我们把使乘积 为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( )
为整数的数n叫做“优数”,则在区间(1,2004)内的所有优数的和为( )
| A.1024 | B.2003 | C.2026 | D.2048 |
已知 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且 是
是 与
与 的等比中项,
的等比中项, 为
为 前
前 项和,
项和, 则
则 的值为( )
的值为( )
| A.-110 | B.-90 | C.90 | D.110 |
设函数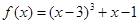 ,数列
,数列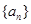 是公差不为0的等差数列,
是公差不为0的等差数列,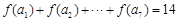 ,则
,则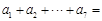 ( )
( )
| A.0 | B.7 | C.14 | D.21 |
设 为等差数列,且
为等差数列,且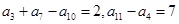 ,则数列
,则数列 的前13项的和为
的前13项的和为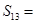
| A.63 | B.109 | C.117 | D.210 |
在等差数列{an}中,首项a1=0,公差d≠0,若am=a1+a2+…+a9,则m的值为( )
| A.37 | B. 36 | C.20 | D.19 |