题目内容
已知双曲线
，过其右焦点且垂直于实轴的直线与双曲线交于
两点，
为坐标原点.若
，则双曲线的离心率为
A． | B． | C． | D． |
D
解析试题分析：
根据题意可得|MF|=|OF|，再利用双曲线的几何性质表示出a，b，c的关系式，进而求得a和c的关系，则双曲线离心率可得．解：设右焦点为F，由条件可得，|MF|=|OF|，即可知为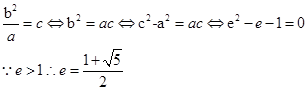
故选D.
考点：双曲线的几何性质
点评：本题主要考查了双曲线的简单性质．考查了直线与圆锥曲线的位置关系．综合考查了学生基础知识的掌握和理解．
练习册系列答案
相关题目
在抛物线
上，横坐标为
的点到焦点的距离为
，则
的值为（ ）
| A．0.5 | B．1 | C．2 | D．4 |
方程
表示焦点在
轴的双曲线，则
的取值范围是（ ）
A． | B． | C． | D． |
设抛物线顶点在坐标原点，，准线方程为
，则抛物线方程是（ ）
A． | B． | C． | D． |
(p >0)的焦点F恰好是双曲线C2:
(a>0,b >0)的右焦点，且它们的交点的连线过点F，则双曲线的离心率为
椭圆
上有n个不同的点：P1，P2， ，Pn，椭圆的右焦点为F，数列{|PnF|}是公差大于
的等差数列，则n的最大值是 （ ）
| A．198 | B．199 |
| C．200 | D．201 |
已知点
、
分别是双曲线
的左、右焦点，过且垂直于
轴的直线与双曲线交于
、
两点，若
为锐角三角形，则该双曲线的离心率
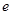的取值范围是
A． | B． | C．（1，2） | D． |
椭圆
的离心率为（ ）
A． | B． | C． | D． |
已知
＜4，则曲线
和
有（ ）
| A．相同的准线 | B．相同的焦点 | C．相同的离心率 | D．相同的长轴 |