题目内容
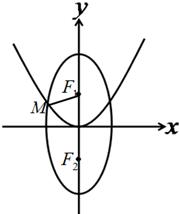
如图,已知F1、F2分别为椭圆C1: 的上、下焦点,其中F1也是抛物线C2:
的上、下焦点,其中F1也是抛物线C2: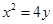 的焦点,点A是曲线C1,C2在第二象限的交点,且
的焦点,点A是曲线C1,C2在第二象限的交点,且

(Ⅰ)求椭圆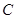 1的方程;
1的方程;
(Ⅱ)已知P是椭圆C1上的动点,MN是圆C: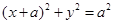 的直径,求
的直径,求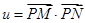 的最大值和最小值.
的最大值和最小值.
(Ⅰ) ;
;
(Ⅱ)当 时,
时, ,当
,当 时,
时, 。
。
解析试题分析:(Ⅰ)抛物线C2的焦点F1(0,1),准线 ,易得
,易得 ∴
∴
∴  (正值舍去)∴
(正值舍去)∴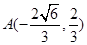 3分
3分
又 ………①
………①  …………② 5分
…………② 5分
联立①②得 ∴椭圆C1的方程为
∴椭圆C1的方程为 6分
6分
(Ⅱ)圆C: ∴圆心C(-2,0),半径
∴圆心C(-2,0),半径
设P(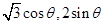 ) 7分
) 7分
法一: 9分
9分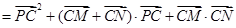
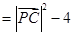
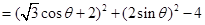
 11分
11分
当 时,
时, 12分
12分
当 时,
时, 13分
13分
法二:设M( ),则N(
),则N(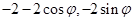 ) 8分
) 8分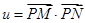
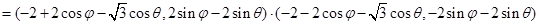

 11分
11分
当 时,
时, 12分
12分
当 时,
时, 13分
13分
法三: 8分
8分
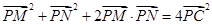
∵C是MN中点,∴ 9分
9分
∴  10分
10分
∴
 11分
11分
当 时,
时, 12分
12分
当 时,
时, 13分
13分
考点:本题主要考查抛物线的几何性质,椭圆的标准方程,椭圆的几何性质,直线椭圆的位置关系,平面向量的坐标运算。
点评:中档题,求椭圆的标准方程,主要运用了椭圆的几何性质,a,b,c,e的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)利用平面向量的坐标运算,将问题转化成三角函数问题,确定最值。

练习册系列答案
相关题目
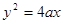 (
(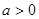 且
且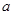 为常数),
为常数),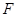 为其焦点.
为其焦点.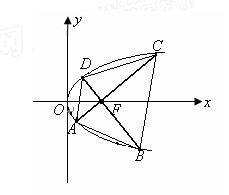
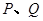 两点,且
两点,且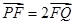 ,求直线
,求直线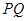 的斜率;
的斜率;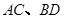 是过抛物线焦点
是过抛物线焦点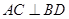 ,如图所示.求四边形
,如图所示.求四边形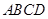 面积的最小值
面积的最小值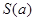 .
.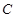 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,其左、右焦点分别为
轴上,其左、右焦点分别为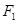 、
、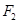 ,短轴长为
,短轴长为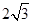 ,点
,点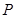 在椭圆
在椭圆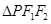 的周长为6.
的周长为6.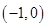 的直线与椭圆相交于A、B两点,试问在x轴上是否存在一个定点M使
的直线与椭圆相交于A、B两点,试问在x轴上是否存在一个定点M使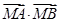 恒为定值?若存在求出该定值及点M的坐标,若不存在请说明理由.
恒为定值?若存在求出该定值及点M的坐标,若不存在请说明理由. ,
,
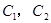 的方程为普通方程,并说明它们分别表示什么曲线?
的方程为普通方程,并说明它们分别表示什么曲线?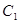 上的点P对应的参数为
上的点P对应的参数为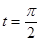 ,Q为
,Q为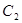 上的动点,求PQ的中点M到直线
上的动点,求PQ的中点M到直线 的距离的最小值
的距离的最小值 的离心率为
的离心率为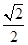 ,且经过点
,且经过点 .
. ,
, 两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且
两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且 .求△ABM的面积.
.求△ABM的面积.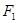 、
、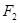 分别为椭圆
分别为椭圆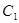 :
: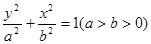 的上、下焦点,其中
的上、下焦点,其中 :
: 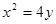 的焦点,点
的焦点,点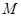 是
是 。
。
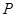 (1,3)和圆
(1,3)和圆 :
: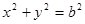 ,过点
,过点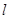 与圆
与圆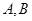 ,在线段
,在线段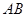 取一点
取一点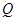 ,满足:
,满足: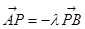 ,
,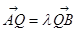 (
(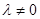 且
且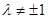 )。
)。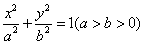 过点
过点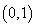 ,其长轴、焦距和短轴的长的平方依次成等差数列.直线
,其长轴、焦距和短轴的长的平方依次成等差数列.直线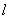 与
与 轴正半轴和
轴正半轴和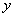 轴分别交于点
轴分别交于点 、
、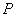 ,与椭圆分别交于点
,与椭圆分别交于点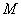 、
、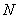 ,各点均不重合且满足
,各点均不重合且满足
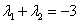 ,试证明:直线
,试证明:直线 )及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为
)及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为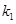 、
、 且
且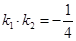
 与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线
与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线 的距离。(O为坐标原点)
的距离。(O为坐标原点)
 ,m
,m 0),点P的轨迹加上M、N两点构成曲线C.
0),点P的轨迹加上M、N两点构成曲线C. ,曲线C过点Q (2,0) 斜率为
,曲线C过点Q (2,0) 斜率为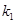 的直线
的直线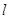 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR (O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR (O为坐标原点)的斜率为 ,求证
,求证 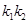 为定值;
为定值; ,且
,且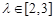 ,求
,求