题目内容
已知不等式4x-5•2x+2+64≤0的解集为A,试求函数f(x)=log2
• log2
(x∈A)的值域.
| x |
| 2 |
| x |
| 4 |
分析:由已知得(2x)2-20•2x+64≤0解不等式可求A,而f(x)=(log2x-1)(log2x-2)=log22x-3log2x+2=(log2x-
)2-
,结合二次函数的性质可求函数的值域
| 3 |
| 2 |
| 1 |
| 4 |
解答:解:由已知得(2x)2-20•2x+64≤0
∴4≤2x≤16,
∴A={x|2≤x≤4}
而f(x)=(log2x-1)(log2x-2)=log22x-3log2x+2=(log2x-
)2-
∵2≤x≤4,∴log2x∈[1,2]
∴f(x)∈[ -
, 0 ]
∴4≤2x≤16,
∴A={x|2≤x≤4}
而f(x)=(log2x-1)(log2x-2)=log22x-3log2x+2=(log2x-
| 3 |
| 2 |
| 1 |
| 4 |
∵2≤x≤4,∴log2x∈[1,2]
∴f(x)∈[ -
| 1 |
| 4 |
点评:本题主要考查了指数不等式 的求解,二次函数在闭区间上的最值的求解,属于中档试题

练习册系列答案
相关题目
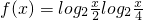 (x∈A)的值域.
(x∈A)的值域.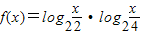 (x∈A)的值域.
(x∈A)的值域.